5. Základy teorie prognóz a prognostika.
V této kapitole si klademe za cíl uvést krátký pøehled metod mnohonásobného zpøesnìní hodnoty urèitého parametru systému. Tento parametr je výstupní charakteristikou modelu. Existují obecnì dva pøístupy. Jeden je založen na existujících údajích a má pomìrnì blízko ke klasické statistice, druhý využívá postupnì získané nové informace a na jejich základì provádí další korekci alternativ.
Sledované charakteristiky jsou dvou základních typù. Jsou to promìnné stavu a promìnné intenzity. Rozlišujeme je podle závislosti na èase. První z nich pøedpovídáme periodicky a jejich hodnota je v krátkém èasovém intervalu stabilní a nezávisí na délce pozorování. Takovými charakteristikami jsou obvykle rychlost, teplota, poèet pøedplatitelù apod. Promìnné intenzity urèujeme periodicky, ale jejich hodnota je závislá na délce pozorování. Takovými charakteristikami jsou napø. množství dešťových srážek, množství prodaných výrobkù atd.
Prognozování tìchto dvou typù charakteristik se od sebe podstatnì liší. Uvedeme si nìkteré základní rozdíly:
1.Provádíme-li mìøení parametrù systému ve stejných èasových intervalech, je velikost tìchto intervalù podstatná pro promìnné intenzity a nepodstatná pro promìnné stavu.
2.Správná pøedpovìï promìnné stavu musí urèovat její hodnotu na konci pøedpovìdního intervalu a pøedpovìï promìnné typu intenzity musí být souètem prognóz z celého pøedpovìdního intervalu.
3.Funkce rozdìlení pravdìpodobnosti správné nebo chybné pøedpovìdi pro promìnnou stavu musí odpovídat funkci rozdìlení chyb výchozích mìøených dat. Funkce rozdìlení chybné nebo správné pøedpovìdi pro promìnnou intenzity je asymptoticky normálním rozdìlením pravdìpodobnosti.
Velmi dùležitou roli v pøedpovìdích hraje správné urèení velikosti jednotlivých èasových intervalù, ve kterých se provádí zpøesnìní nebo korekce pøedpovìdi. Podstatný rozdíl by mìl být mezi velikostí intervalu pro prognózy tìžby døeva v lese s dobou obnovy 80 let a prognózováním spotøeby elektrické energie bìhem dne. U prognózování tìžby v lese je dostateèná perioda upøesnìní 10 let, u spotøeby elektrické energie by to mohla být každá hodina.
Metody pøedpovìdí mùžeme rozdìlit do tøí skupin:
A. Statistické pøedpovìdi.
B. Kauzální pøedpovìdi.
C. Kombinované metody pøedpovìdí.
A. Statistické pøedpovìdi.
Statistické pøedpovìdi jsou založeny na údajích za urèitá období a vytváøí obvykle hypotézy o možných extrémech èasových závislostí jednotlivých promìnných v systému a také o hodnotách tìchto promìnných v extremálních bodech. Metodami jsou pøedevším regresní analýza,analýza èasových øad. Z matematických metod pøedevším metoda nejmenších ètvercù.
B.Kauzální pøedpovìdi.
Pøedpovìdi na základì kauzálních (pøíèinných) vztahù se využívají pøevážnì k prognóze momentu extrému a jeho hodnoty.
Metody teorie prognóz jsou dùležitou èástí všech plánovacích a rozhodovacích procesù. Jedná se o pøedvídání chování trhu, pohybu cen, poptávky, odbytu apod.
Výchozí údaje jsou obvykle výsledkem øady systematických nebo nahodilých pozorování. Výsledky tìchto pozorování jsou registrovány a èasto obsahují øadu nahodilých i systematických chyb. První úlohou je se tìchto chyb zbavit. Kromì chyb se mohou v pozorováních vyskytovat i anomální jevy, které jsou z hlediska prognózy vývoje nepodstatné. Napø. nenormálnì vysoká poptávka pøi stávkách nebo neobyèejnì vysoká teplota, která byla zaregistrována pøi pøehøátí termoregulátoru.
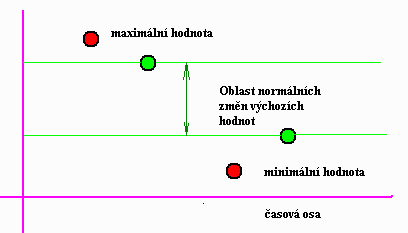
Z tìchto hledisek není vhodné všechny informace zaøazovat do podkladù dobré pøedpovìdi. Øíkáme, že èasovou filtrujeme. Vyluèujeme ty hodnoty, které necharakterizují prognózovaný proces. Jeden z možných jednoduchých zpùsobù filtrace je zobrazen na následujícím obrázku 33.
poptávka

Obr.33
Pro ekonomické údaje, které jsou èasto charakteristické exponenciálními závislostmi, využíváme logaritmické mìøítko. Jinou efektivní metodou je rozdìlení výchozí èasové øady na èásti a prognózování na jednotlivých èástech èasové øady. Tento postup používáme napø. pøi prognózách poptávky.
Libovolný proces, který popisujeme øadou výsledkù jednotlivých pozorování, mùžeme schématicky popsat matematickým modelem. Tento model obvykle obsahuje soubor diferenèních nebo diferenciálních rovnic.
5.1. Metody klasické statistiky v teorii prognóz.
A. Regresní analýza.
Regresní analýza se provádí na základì údajù za pøedcházející období. Jejím cílem je získání vztahù a závislostí mezi nìkolika promìnnými. Pøedpokládejme, že existuje nìjaká závislost mezi promìnnou y a promìnnými x1,x2,...,xp. Vytvoøíme tedy napø. rovnici lineární regrese
y = b0 + b1 * x1 + b2 * x2 + ...+ bp * xp + z,
kde z je chyba, obvykle s marginálním rozdìlením pravdìpodobnosti. Pro urèení parametrù modelu z namìøených hodnot použijeme metody nejmenších ètvercù.
Používat regresní funkce je možné pouze pøi splnìní následujících pøedpokladù:
- regresní rovnice je strukturní a zùstává pravdivou po celou dobu pøedpovìdi
- argumenty regresní funkce nelze v dobì pøedpovìdi dostateènì ocenit
- funkce rozdìlení pravdìpodobnosti chyby zùstává i v budoucnu stejná
Z tìchto podmínek je zøejmé, že regresní funkce mùžeme využívat pouze opatrnì.
Pøíklad.
Prùzkum spotøeby elektrické energie ukázal, že je možné použít regresní funkci v logaritmickém mìøítku.
IE - ukazatel spotøeby elektrické energie
IN - ukazatel tvorby národního dùchodu
IP - ukazatel prùmyslové výroby
Souvislost jednotlivých ukazatelù ukazuje následující rovnice regrese
ln ( IE ) = a0 + a1 * ln ( IP ) + a2 * ln ( IN )
Bohužel, zjistilo se, že se tento vztah èasem
mìní
a proto je využitelný pro prognózu v
období max. 5
- 6 let. Za období let 1965-1970 byly
shromáždìny
podklady, a na jejich základì byla sestavena
regresní
funkce a následnì prognóza na rok
1971. Vypoèítané
hodnoty byly následující:
IN = 835 a0 = 1.25 a1 = 0.34 a2 = 0.336
IP = 2630
Prognózovaná hodnota èinila 513 jednotek a skuteènost byla 253. Tedy rozdíl dosti znaèný.
Následující program ilustruje použití metody nejmenších ètvercù.
PROGRAM NEJMENSI_CTVERCE;
USES PRINTER;
LABEL 99;
CONST MI=1E-6;
TYPE MAT=ARRAY[1..100,1..100] OF REAL;
VAR M,N,ND,MD,I,J,K,K1,N1:INTEGER;
T,MAX:REAL;S:BOOLEAN;A:MAT;Z:ARRAY[1..100] OF REAL;
X,Y:ARRAY[1..100] OF REAL;
BEGIN WRITE('ZADEJ POCET HODNOT:');READLN(M);
WRITE('ZADEJ STUPEN POLYNOMU:');READLN(N);N:=N+1;
WRITELN('ZADEJ HODNOTY X A Y');
FOR I:=1 TO M DO READLN(X[I],Y[I]);
FOR I:=1 TO N DO FOR J:=1 TO N+1 DO A[I,J]:=0;
FOR I:=1 TO N DO BEGIN FOR J:=1 TO N DO FOR K:=1 TO M DO IF X[K]<>0 THEN
A[I,J]:=A[I,J]+EXP((I-1)*LN(ABS(X[K])))*X[K]/ABS(X[K])*EXP((J-1)*LN(ABS(X[K])))*X[K]/ABS(X[K]) ELSE
IF (I-1=0) AND (J-1=0) THEN A[I,J]:=A[I,J]+1;
FOR K:=1 TO M DO IF X[K]<>0 THEN
A[I,N+1]:=A[I,N+1]+Y[K]*EXP((I-1)*LN(ABS(X[K])))*X[K]/ABS(X[K]) ELSE
IF I-1=0 THEN A[I,N+1]:=A[I,N+1]+ Y[K] END;
ND:=N;MD:=N+1;
FOR I:=1 TO ND DO BEGIN FOR J:=1 TO MD DO WRITE(LST,A[I,J]:9:2);WRITELN(LST) END;
S:=FALSE;N1:=N+1;K:=1;
WHILE K<N DO BEGIN FOR J:=K TO N DO BEGIN MAX:=0.0;
FOR I:=K TO N DO BEGIN T:=A[I,J];IF ABS(T)>ABS(MAX) THEN MAX:=T END;
S:=(MAX>-(MI)) AND (MAX<MI);
IF S THEN GOTO 99;
FOR I:=K TO N1 DO A[J,I]:=A[J,I]/MAX END;MAX:=0.0;
FOR I:=K TO N DO BEGIN T:=A[I,K];IF ABS(T)>ABS(MAX) THEN BEGIN MAX:=T;
J:=I END END;
S:=(MAX>-(MI)) AND (MAX<MI);
IF S THEN GOTO 99;
IF J<>K THEN FOR I:=K TO N1 DO BEGIN T:=A[J,I];A[J,I]:=A[K,I];A[K,I]:=T END;
K1:=K+1;FOR I:=K1 TO N DO BEGIN T:=A[I,K]/MAX;
FOR J:=K1 TO N1 DO
A[I,J]:=A[I,J]-T*A[K,J] END;K:=K+1 END;
I:=N;
REPEAT Z[I]:=A[I,N1]/A[I,I];K:=I-1;
FOR J:=1 TO K DO A[J,N1]:=A[J,N1]-Z[I]*A[J,I];I:=K
UNTIL K=0;
99:IF S THEN WRITELN('TAKOVOU SOUSTAVU NERESIM!!!') ELSE BEGIN
WRITELN(LST,'RESENI: KOEFICIENTY JSOU USPORADANY OD NEJ.MOCNINY X^0');FOR I:=1 TO ND DO BEGIN T:=Z[I];
WRITELN(LST,'X(',I:3,') =',T:9:5) END END END.
B. Analýza èasových øad.
Úlohou statistické analýzy je vyjasnìní charakteristik èasové øady ukazatele xt. V pøípadì multiplikativního modelu pøedpokládáme, že
xt = Tt * ct * St + et
Tt - je trend vývoje, obyèejnì jej vyjadøujeme jako polynom, exponentu apod.
ct - cyklická èást prognózy
St - sezónní vlivy
et - chyba
Urèovat trendy, cyklické a sezónní vlivy umí nìkteré statistické systémy napø. systém STATGRAF apod. Uvedeme si opìt alespoò jeden pøíklad.
Pøíklad.
Pøi analýzách výrobního trendu v malém závodì byly získány za posledních pìt let následující údaje v jednotlivých mìsících (údaje jsou zobrazeny po øádcích):
| 508 | 515 | 524.2 | 528 | 530.7 | 543.7 | 542.8 | 550 | 559 | 564.3 | 569.6 | 581.2 |
| 582.6 | 589.9 | 601.2 | 606.6 | 619.2 | 614.8 | 624.9 | 634.5 | 639.6 | 645.5 | 648.8 | 658.7 |
| 661.6 | 667.2 | 676.7 | 682 | 688 | 693.9 | 700 | 711.2 | 716.1 | 724 | 727.9 | 742.6 |
| 741.1 | 749.9 | 756.2 | 760.7 | 763.1 | 773.2 | 777.5 | 783.6 | 790.6 | 799.2 | 802.6 | 805.9 |
| 808.4 | 820.8 | 823.8 | 831.2 | 835.5 | 837.4 | 846.7 | 854.2 | 859.9 | 867. | 871.3 | 876.5 |
Abychom mohli urèit napø. trend, musíme vypoèítat následující charakteristiky. Zavedeme oznaèení:
/\ xt = xt+1- xt, analogicky diference vyšších øádù
/\ k+1 xt = /\ k xt+1 - /\ k xt.
Dále Var ( /\ k xt ) = (2*k+2)! * d2/ ((k+1)!)2.
Pro jednotlivá "k" získáme hodnoty
| Hodnota K | /\ k |
| 1 | 14.238 |
| 2 | 7.7078 |
| 3 | 4.05 |
| 4 | 3.85 |
Z tìchto hodnot vidíme, že trendem je polynom druhého stupnì. Variace diferencí se pak již podstatnì nemìní. Z tìchto hodnot mùžeme metodou nejmenších ètvercù získat vztah:
xt = 508 + 6.3 * t - 0.004 * t2 + et
Nemùžeme však s jistotou tvrdit, že i v
budoucnu bude tento trend
zachován.
A.Metoda exponenciálního vyrovnávání.
Pøi sestavování pøedpovìdí na základì èasové øady s nedostateèným poètem èlenù se èasto používají nìkteré jednoduché adaptivní metody. Jednou z tìchto metod je i metoda exponenciálního vyrovnávání.
Prognóza, získaná touto metodou je teoreticky stabilní a souèasnì citlivá ke zmìnám koeficientù modelu. Je možné ji regulovat výbìrem koeficientu odezvy a, který zavedeme pozdìji. Øada organizací využívá tuto metodu k pøedpovìdi odbytu svých výrobkù.
Pøedpokládejme, že je tøeba pøedpovìdìt odbyt výrobkù za (t+1) mìsíc na základì údajù o odbytu za pøedcházejících "r" mìsícù. První, co nás musí napadnout je, vzít prostì prùmìrný odbyt a ten považovat za pøedpovìï pro další období.
xt+1 = ( xt-r+1 + ...+ xt) / r
Bohužel se ukazuje, že toto èíslo se za prognózu vùbec nehodí. Je to zpùsobeno tím, že skuteènost závisí více na posledním mìsíci nebo roku, než na tom, co bylo pøed sto lety. Proto je rozumné brát "vážený prùmìr". Prognóza pak bude matematicky vypadat takto:
yt = a1 * xt + a2 * xt-1 + ...+ ar * xt-r+1
Logicky by mìlo platit, že koeficienty ai jsou uspoøádány podle velikosti a1>a2>...>ar .Váhové koeficienty mùžeme samozøejmì vybírat nejrùznìjším zpùsobem. V ekonomických aplikacích se osvìdèily pøedevším koeficienty v exponenciálním tvaru.
a2 = ( 1 - a ) * a1,a3 = ( 1 - a ) * a2,...
V tìchto vztazích je a konstanta, kterou nazýváme koeficientem odezvy. Pro velké hodnoty "r" plyne, že
a1 = a , a2 = ( 1 - a ) * a, ....
Dále budeme rozlišovat následující promìnné:
xt - skuteèná hodnota prognózované velièiny v èase t
yt - prognózovaná hodnota velièiny pro èas t.
et - chyba pøedpovìdi v èase t.
Pøi tìchto oznaèeních mùžeme pøedpovìï vyjádøit matematicky následujícím vzorcem:
yt+1 = ( 1 - a ) * yt + a * xt = yt + a * ( xt - yt) = yt + a * et
Pøíklad.
Pokusíme se využít metodu exponenciálního vyrovnávání pro prognózu odbytu betonu v urèité oblasti. (Hodnoty jsou uvádìny v tis.tun)
Koeficient odezvy byl zvolen 0.6.
| Mìsíc | Faktický odbyt | Prognoza | Chyba pøedpovìdi |
| leden | 82,3 | -- | -- |
| únor | 75,4 | 82,3 | -6,9 |
| bøezen | 83,2 | 78,16 | 5,54 |
| duben | 82,9 | 81,48 | 1,42 |
| kvìten | 89,8 | 82,33 | 7,47 |
| èerven | 86,0 | 86,81 | -0,81 |
| èervenec | 77,2 | 86,32 | -9,13 |
| srpen | 79,5 | 80,85 | -1,35 |
| záøí | 81,0 | 80,04 | 0,96 |
| øíjen | 72,3 | 80,62 | -8,32 |
| listopad | 73,6 | 75,62 | -2,02 |
| prosinec | 83,3 | 74,41 | 8,89 |
Z tabulky je zøejmé, že prognózu pro poèáteèní období mùžeme pouze uhádnout. V dalších obdobích se øídíme vznikající chybou. Koeficient odezvy urèujeme subjektivnì a tento koeficient zùstává konstantním po celou dobu prognózy. Pomìrnì øídké zmìny znaku chyby v tabulce jsou zpùsobeny tím, že metoda nedovede vyjasòovat sezónní výkyvy zmìn produkce. Obecným nedostatkem metody je, že mùže ukazovat tendenci k rùstu, i když hodnoty zcela zøejmì klesají.
Zpìtnì by bylo možné urèit optimální koeficient odezvy. Tento koeficient by èinil 0.4508. Musíme si ale uvìdomit, že tabulka vznikala postupnì a apriori nebyl žádný dùvod domnívat se, že koeficientem odezvy bude optimálnì toto magické èíslo.
B.Metoda R.G.Browna-R.Meyera.
Metoda exponenciálního vyrovnávání byla zpracována pro zvláštní pøípad, kdy informace o dynamice zmìn koeficientu odezvy chybí. Jestliže je prognózovaná velièina zatížena velkými fluktuacemi, tato metoda dokáže urèovat již probìhlé zmìny. Proto je rozumné doplnit metodu tak, aby koeficient odezvy byl funkcí èasu. V posledních letech byla navržena celá øada metod zmìny koeficientu odezvy. První z nich je metoda Browna-Meyera. Metoda je založena na periodické zmìnì koeficientu odezvy. Nová hodnota se urèuje jako podíl dvou standardních odchylek:
a2 = E ( /\ yt) / E ( e2t)
Kdy provedeme úpravu koeficientu, urèujeme nejrùznìjším zpùsobem. Buïto pravidelnì nebo v pøípadech rùstu chyby.
PROGRAM BROWN_MEYER;
VAR X,Y,E,ALPA:ARRAY[1..20] OF REAL;
P,S:REAL;N,I,J:INTEGER;
F:TEXT;
BEGIN WRITE('ZADEJ POCATECNI UDAJE : N,ALPA,E(1),Y(1) ');
READLN(N,ALPA[1],E[1],Y[1]);ASSIGN(F,'BROWN.TXT');REWRITE(F);
FOR I:=2 TO N DO BEGIN WRITE(I:2, 'X = ');READLN(X[I]);
Y[I]:=Y[I-1] + ALPA[I-1]*E[I-1];
E[I]:=X[I]-Y[I];
P:=0.0;S:=0.0;
FOR J:=2 TO I DO BEGIN
S:=S+SQR(Y[J]-Y[J-1]);
P:=P+SQR(E[J]-E[J-1]);
END;
ALPA[I]:=SQRT(S/P);
END;
WRITELN(F,'PERIODA PROGNOZA SKUTECNOST CHYBA ALPA ');
FOR I:=2 TO N DO
WRITELN(F,I:6,Y[I]:13:4,X[I]:12:4,E[I]:14:4,ALPA[I]:10:6);
END.
Výsledky programu:
PERIODA PROGNOZA SKUTECNOST CHYBA ALPA
2 82.5500 75.4000 -7.1500 0.032680
3 82.3163 83.7000 1.3837 0.029858
4 82.3577 82.9000 0.5423 0.029994
5 82.3739 89.8000 7.4261 0.025760
6 82.5652 86.0000 3.4348 0.028227
7 82.6622 77.2000 -5.4622 0.024521
8 82.5282 79.5000 -3.0282 0.025545
9 82.4509 81.0000 -1.4509 0.025844
Tento pøíklad pouze ilustruje zmìnu koeficientù odezvy v uvedené metodì.
C.Metoda Trigga-Leache.
Trigg s Leachem navrhli metodu vyhledávacích signálù pro obnovu koeficientù odezvy pro každý èasový okamžik. Díky své jednoduchosti je metoda dosti èasto používaná. Jedná se v podstatì o dvoukrokovou metodu. V prvním kroku probíhá vyrovnání chyby s libovolným koeficientem odezvy:
e'(t) = ß * et + ( 1 - ß ) * e'(t-1)
mt = ß * e'(t) + ( 1 - ß ) * mt-1
Parametr odezvy vybíráme obvykle z intervalu (0.1 ; 0.3 ). Podle definice vyhledávacího signálu získáme
Tt = e'(t) / mt a a = V abs( Tt) .
Ponìkud
upravený program metody:
PROGRAM TRIGG_LEACH;
VAR X,Y,E,ALPA:ARRAY[1..20] OF REAL;
P,S,BETA,ESTR,MSTR:REAL;N,I,J:INTEGER;
F:TEXT;
BEGIN WRITE('ZADEJ POCATECNI UDAJE : N,Y(1) ');
READLN(N,Y[1]);ASSIGN(F,'TRIG.TXT');REWRITE(F);
ESTR:=0.0;MSTR:=1.0;BETA:=0.2;ALPA[1]:=0.5;E[1]:=0.1;
FOR I:=2 TO N DO BEGIN WRITE(I:2, 'X = ');READLN(X[I]);
Y[I]:=Y[I-1] + ALPA[I-1]*E[I-1];
E[I]:=X[I]-Y[I];
ESTR:=BETA*E[I]+(1-BETA)*ESTR ;
MSTR:=BETA*ESTR+(1-BETA)*MSTR;
ALPA[I]:=SQRT(ABS(ESTR/MSTR))/I;
END;
WRITELN(F,'PERIODA PROGNOZA SKUTECNOST CHYBA ALPA ');
FOR I:=2 TO N DO
WRITELN(F,I:6,Y[I]:13:4,X[I]:12:4,E[I]:14:4,ALPA[I]:10:6);
CLOSE(F);
END.
Výsledky testu:
PERIODA PROGNOZA SKUTECNOST CHYBA ALPA
2 82.3500 75.4000 -6.9500 0.815910
3 76.6794 83.7000 7.0206 0.261121
4 78.5126 82.9000 4.3874 0.339353
5 80.0015 89.8000 9.7985 0.329083
6 83.2260 86.0000 2.7740 0.236402
7 83.8818 77.2000 -6.6818 0.120273
8 83.0782 79.5000 -3.5782 0.020659
9 83.0042 81.0000 -2.0042 0.077861
10 82.8482 72.3000 -10.5482 0.425712
11 78.3577 73.6000 -4.7577 0.225140
12 77.2865 83.3000 6.0135 0.113301