Ve většině případů se snažíme v první fázi o získání modelu, který by byl svojí podstatou co nejjednodušší. Jsou reálné předpoklady se domnívat, že jednodušší model bude i snáze řešitelný. Pokud se obrátíme pro ilustraci do matematické analýzy, uvidíme, že obecná funkce se obvykle zkoumá v okolí určitého bodu pomocí své derivace. Jde ve své podstatě o záměnu jedné funkce (původní) jinou funkcí, která je lineární v blízkém okolí bodu.
Je proto možné předpokládat, že i v oblasti modelování bude nejjednodušším přiblížením nějaké reálné závislosti mezi prvky modelovaného systému přiblížení lineární. Pokud budeme tímto způsobem postupovat, budeme vytvořené modely nazývat lineárními modely.
Velké množství technických, ekonomických, biologických a jiných problémů je možné dostatečně přesně popsat lineárními modely. Většina dále uváděných modelů jsou tzv. ekonomicko- matematické modely. Nazývají se tak proto, že obsahují ekonomický ukazatel - cenu. Tuto situaci objasňujeme především tím, že celá oblast lineárního programování vznikla jako nástroj řešení právě modelů tohoto typu.
Rozeberme si nyní jednu současně aktuální úlohu, jejíž historie sahá až k samým kořenům operačního výzkumu. Jedná se o setavení dietního jídelníčku, který by byl při splnění určitých požadavků na výživu současně nejlevnějším. Podobné úlohy vznikají v oblastech, kde je nutné uspokojit stravou obecně velké množství lidí nebo zvířat, např. v armádě, nemocnicích, závodních jídelnách, velkovýkrmnách hospodářských zvířat apod.
Předpokládejme, že je znám seznam dostupných potravin, které můžeme zakoupit a tento seznam obsahuje obecně n-položek (chléb, cukr, sůl, máslo, sýr, mléko, rýže, mouka, brambory, olej atd.). To, co momentálně provádíme, je první fáze tvorby modelu a sice vyčlenění systému prvků na objektu modelování. Potraviny označíme P1,P2,...,Pn. Mimo to budeme dále předpokládat, že existují takové charakteristiky jednotlivých potravin, jako jsou vitaminy, minerální látky, cukry, tuky, bílkoviny, kalorická hodnota atd. Předpokládejme, že těchto charakteristik je m.
Tyto charakteristiky označme písmeny N1,N2,...,Nm. Dále budeme předpokládat, že jsou známy obsahy těchto charakteristik v jednotlivých potravinách. Přesně řečeno, předpokládáme, že je znám obsah charakteristiky i v potravině j a označme ho jako aij. V tomto případě můžeme vytvořit následující tabulku:
| P1 | P2 | P3 | P4 | ... | |
| N1 | a11 | a12 | a13 | a14 | ... |
| N2 | a21 | a22 | a23 | a24 | ... |
| ... | ... | ... | ... | ... | aij |
Prvky této tabulky tvoří matici, kterou si můžeme označit písmenem A. Matice je složena z m řádků a n sloupců.
Předpokládejme, že jsme sestavili jídelníček x = ( x1,x2,...,xn) na určité období ( měsíc, rok, ...). Jinými slovy jsme naplánovali na toto období x1 potraviny P1, x2 potraviny P2, atd. Poměrně jednoduše můžeme vypočítat, kolik vitamínů, tuků, bílkovin a minerálních látek získá člověk za toto období z těchto potravin:
(2.1) a11 * x1 + a12 * x2 + ...+ a1n * xn = ( a1,x )
Na pravé straně výrazu 2.1 je skalární součin prvního řádku matice A s vektorem x. Analogicky můžeme postupovat pro ostatní charakteristiky. Celkově tedy můžeme vyjádřit všechny charakteristiky v maticové podobě jako součin matice A a vektoru x:
(2.2) A.x = bs ,
kde bs vyjadřuje vektor skutečného obsahu charakteristik v jídelníčku.
Předpokládejme, že existují přesně stanovené lékařské požadavky, týkající se potřebného množství jednotlivých komponent v zadaném jídelníčku. Například množství vitamínu C v jídelníčku na jeden den nesmí být menší než 50mg na den. Všechny tyto požadavky můžeme charakterizovat vektorem b. Toto pak matematicky znamená, že vektor x musí vyhovovat následujícímu požadavku:
(2.3) A .x >== b
Mimo to je ze zadání úlohy zřejmé, že vektor x jídelníčku může obsahovat pouze nezáporné komponenty. Tuto podmínku můžeme zformulovat také tak, že vektor x je větší nebo roven nulovému vektoru. Pojem větší nebo roven chápeme po_jednotlivých_souřadnicích. Doplníme tedy podmínku 2.3 o podmínku
(2.3a) A .x >= b a x >= 0
Pokud bychom fakt nezápornosti jídelníčku nezachytili ve fázi formalizace úlohy, dále by nás už žádná matematika nezachránila. V matematickém modelu již o smyslu jednotlivých proměnných neuvažujeme.
Doposud bylo zřejmé, že libovolný jídelníček, který chceme realizovat, musí vyhovovat podmínkám 2.3a, přesto takovýchto jídelníčků může být nekonečně mnoho. Dalším krokem, který musíme udělat, je zformulovat cíl operace. V této fázi ustoupí dietní lékař své místo finančníkovi. Musíme přidat do systému prvků pojem jednotkové ceny jednotlivých potravin. Nechť tedy je dále známa jednotková cena jednotlivých potravin.Cena potraviny P1 je c1, cena potraviny P2 je c2 atd. To znamená, že celková cena jídelníčku může být vyjádřena ve tvaru:
(2.4) c1.x1 + c2.x2 + ...+ cn.xn = (c,x)
Nyní tedy můžeme slovně zformulovat úlohu o dietě takto: "Mezi vektory x,které vyhovují omezením 2.3a, vyberte takový, pro který nabývá výraz 2.4 nejmenší hodnotu."
Matematický model pro úlohu o dietě můžeme zformulovat následovně:
(2.5) m i n ( c , x )
A .x >= b , x >= 0
Zhodnoťme nyní dosažený výsledek. Vyjádřili jsme reálnou úlohu v přísně matematickém tvaru a to nám v blízké budoucnosti umožní využít pro její řešení bohatý matematický aparát. Z druhé strany ve vzorcích 2.5 jsme se zcela abstrahovali od původního smyslu úlohy a jestliže jsme opomněli některé podstatné rysy modelu, pak by ani matematicky přesné řešení nedalo správný výsledek.
Je jasné, že náš jednoduchý model zdaleka neodráží všechna úskalí reálné úlohy. Například mohou být i omezení, která určují, že některé charakteristiky potravin nesmějí převyšovat určitá množství. Je třeba říci, že takováto omezení je jednoduché akceptovat. Mimo to však v omezeních mimo lékaře mohou figurovat i aspekty, vybíravost člověka, chuť a jiné.
Dalším podstatným nedostatkem je, že není zaručeno, že z potravin, které budou vybrány pro jídelníček, je možné sestavit jedlý pokrm.
Jako ilustraci si uveďme, že v roce 1945 byla uveřejněna zpráva o výsledcích řešení úlohy o dietě s konkrétními číselnými parametry: Bylo zavedeno 77 druhů potravin a 9 charakteristik. Řešila se úloha o dietě jednoho člověka na období jednoho roku. Optimální řešení bylo získáno simplexovou metodou a obsahovalo pouze 9 ze 77 potravin. Byly to tyto potraviny : mouka, kukuřice, kondenzované mléko, rostlinný tuk, sádlo, hovězí játra, zelí, brambory a špenát.
Optimální dieta stála ve své době 39 dolarů a 67 centů a byla absolutně bez chuti , a proto nepřijatelná.Jídelníček, sestavený dietním lékařem, byl plně uspokojivý a stál 115 dolarů.
Nehledě na tento zajímavý a poučný příklad nezdařeného experimentu, nemůžeme učinit závěr, že výše uvedený model dává nevyhovující řešení. V prvé řadě můžeme zavést omezení na objem spotřeby jednotlivých potravin, dále můžeme použít i jiné metody, než je metoda simplexová a dosáhnout větší bohatosti jídelníčku.
Existuje však celá řada oblastí,kde daný model můžeme použít naprosto bez jakýchkoliv změn. Model byl a je využíván při přípravě krmných směsí pro dobytek, k sestavování směsí naftových derivátů apod.
Nechť je zadáno m míst S1 ,S2 , ...,Sm výroby homogenního výrobku (uhlí, cementu, hnojiv, mouky apod.).Předpokládejme, že jeho produkce v místě Si činí ai jednotek (kg, litrů, tun ). Předpokládejme, že se tento výrobek spotřebovává v n místech Q1 ,Q2 , ...,Qn. Jeho spotřeba v místě Qj je bj jednotek.
Cílem operace je setavit takový plán přepravy homogenního produktu z míst S do míst Q , abychom uspokojili spotřebu, nepřekročili produkci a minimalizovali přepravní náklady. Abychom mohli pokračovat ve formalizaci této úlohy, potřebujeme znát ještě některé další údaje. Nechť cij je cena potřebná na přepravu jedné jednotky výrobku z místa jeho výroby Si do místa jeho spotřeby Qj .Budeme dále předpokládat, že přepravní náklady závisí lineárně na přepravovaném množství (což obecně není velmi často pravda).
Plánem přepravy budeme nazývat soubor čísel ( xij)i=1,2,...,m ,který vyhovuje následujícím podmínkám: j=1,2,...,n
(2.6) ![]() xij
= ai a
xij
= ai a ![]() xij
= bj a xij>= 0
xij
= bj a xij>= 0
j=1,2,...,n i=1,2,...,m
Podstata jednotlivých rovnic je zřejmá. Z místa Si se musí vyvést právě tolik produkce, kolik se tam vyrobí a do místa Qj se musí dovést právě tolik, kolik se tam spotřebuje. Není možné přitom převážet záporné množství materiálu. Toto je však možné pouze tehdy, když je dopravní problém vyrovnaný nebo jinými slovy, když platí:
(2.7) ![]() ai
=
ai
= ![]() bj
bj
i=1,2,...,m j=1,2,...,n
Při plánu přepravy x můžeme potom vyjádřit celkové přepravní náklady vztahem:
(2.8) ![]() cij
* aij
cij
* aij
i=1,2,...,m a j=1,2,...,n
Konečná formulace matematického modelu dopravní úlohy tedy je:
"Na množině všech souborů čísel, která vyhovují podmínkám 2.6 najděte takový soubor x, který minimalizuje vztah 2.8."
Dopravní problém byl jednou z prvních úloh,která přinesla ekonomicky poměrně velký efekt. Je třeba si však uvědomit, že ušetření nákladů řešením dané optimalizační úlohy obecně vede k jiným nákladům a to nákladům na vlastní řešení optimalizační úlohy. Bylo by směšné, kdybychom pro halířové úspory, které někdy mohou vzniknout, vynaložili desetitisíce na řešení optimalizační úlohy. Tento fakt je třeba mít neustále na paměti!!!
Nechť je dáno m zemědělských pozemků, které označíme S1, S2 ,...,Sm,připravených k pěstování různých zemědělských kultur. Tyto pozemky se liší charakterem půdy, svým umístěním apod. Na každém pozemku má být zaseta jedna nebo několik z celkem n zemědělských kultur Q1 ,Q2 ,...,Qn (pšenice, žito, oves, řepa, brambory apod.). Budeme předpokládat, že je znám výnos z hektaru kultury Qj na poli Si a je roven aij. Označme plochu pozemku Si v hektarech jako pi. Úlohu o racionálním využití osevních ploch můžeme zformulovat takto:
Je určen plán výroby bj každé jednotlivé plodiny Qj. Jsou známy nákupní ceny cj pro každou jednotku produkce plodiny Qj. Máme určit plán osevů osevních ploch tak, aby zisk z prodeje vypěstovaných zemědělských produktů byl maximální.
Označme xij plochu v hektarech,kterou zaujímá kultura Qj na poli Si. V takovém případě bude matematický model výše zformulované úlohy vypadat následovně:
(2.9) m a x [ ![]() cj * (
cj * ( ![]() aij * xij)]
aij * xij)]
| 1<=j<=n | 1<=i<=m |
![]() xij =
pi ,
xij =
pi , ![]() aij * xij
= bj , xij >= 0
aij * xij
= bj , xij >= 0
| 1<=j<=n | 1<=i<=m |
Budeme nyní analyzovat činnost určité hospodářské jednotky ( firmy, dílny, závodu apod.). Naším úkolem je sestavit takový plán výroby, který v maximální možné míře zabezpečí zisk z prodeje vyrobených výrobků.
Předpokládejme, že jsou známy technologické možnosti dané výrobní jednotky a také množství surovin a jiných zdrojů,které můžeme čerpat. Nechť existuje m druhů surovin, které jednotka využívá pro výrobu své produkce, označme je písmeny R1 ,R2 ,...Rm. Těmito surovinami mohou být kovy, uhlí, ruda, elektrická energie, finance, ale i pracovní síla apod. Předpokládejme dále, že v naší výrobní jednotce můžeme vyrábět n druhů různých výrobků, které můžeme označit analogicky G1,G2,..., Gn.
Technologií výroby výrobku Gj budeme nazývat soubor čísel (aij)i=1,2,...m, který určuje, jaké množství suroviny Ri jsou nutná pro výrobu jednotky výrobku Gj. Takovým způsobem můžeme výrobu chápat jako posloupnost, ve které dodáváme postupně jednotlivé suroviny v množstvích a1j , a2j , ..., amj a na konci tohoto procesu vychází hotový výrobek.
Na základě těchto informací můžeme sestavit takzvanou technologickou matici výroby.
Tato matice plně popisuje současnou technologii výroby dané výrobní jednotky. Nechť jsou dále zadána množství bi surovin Ri, která mohou být využita ve výrobě. Označme symbolem b vektor těchto surovin. Plánem výroby nazveme vektor x = (x1,x2,...,xn), který ukazuje jaká množství jednotlivých výrobků mohou být vyrobena.
(2.10)
| G1 | G2 | ... | Gl | ... | Gn | |
| R1 | a11 | a12 | ... | a1j | ... | a1n |
| R2 | a21 | a22 | ... | a2j | ... | a2n |
...
Zbývá předpokládat, že technologie výroby je lineární, to znamená, že spotřeba surovin je přímo úměrná objemu výroby. Pokud budeme považovat vektor c za vektor cen hotové produkce, pak matematický model této úlohy bude mít následující tvar:
(2.11) m a x (c , x )
A.x <= b ,x >= 0
Pokud se plánování vede v nomenklatuře, pak může být zformulována i jiná úloha. Nechť je dán vektor x, který definuje kompletní výrobek. Například jedno auto = (4 kola,1 volant, 2 světla atd.). Úlohou je sestavit co nejvíce kompletních výrobků.
Označme počet těchto kompletních výrobků, potom můžeme řešit následující optimalizační úlohu:
(2.12) m a x
A.x <= b , x >= .x , x >= 0
Nerovnice x>= .x znamená, že vektor x obsahuje nejméně úplných kompletů výrobků. Předchozí dva modely odrážejí určité rysy reálného procesu výroby, jsou však současně i značně idealizované, protože jim chybí to nejzávažnější a to je čas.
Počítali jsme také s tím, že všechny suroviny máme k dispozici a technologie výroby je neměnná. Ve skutečnosti je situace poněkud složitější.
Základem mnohých modelů lineárních procesů jsou schemata meziodvětvové výměny. Jim a jejich modifikacím je věnována velmi široká odborná literatura.
Celou výrobní oblast ekonomiky rozdělíme do n čistých odvětví. Jinými slovy to znamená, že takovéto odvětví vyrábí homogenní produkci."Čisté" odvětví je určitá idealizace ekonomického prostředí a není ani důležité, aby tento pojem v nějakých reálných formách existoval. Z jedné strany tato idealizace jistě omezuje model, ale z druhé strany taková je nutná k provedení detailní ekonomické analýzy technologické struktury společenské výroby a rozdělování.
Vraťme se nyní opět k našemu modelu. Předpokládejme, že každé odvětví vyrábí výrobek jednoho typu a různá odvětví vyrábějí různé výrobky. V takovém modelu výrobně-ekonomické sféry figuruje tedy n-typů výrobků. V procesu výroby každé odvětví zpracovává a spotřebovává výrobky ostatních odvětví.
Předpokládejme nyní, že v nějakém časovém okamžiku T0 byla podle výsledných položek sestavena bilance výrobků za určité období (např. za jeden kalendářní rok). Hodnoty prvků aij v následující tabulce ukazují objem výrobku i spotřebovaný odvětvím j za toto období. Číslo Vj ukazuje objem výroby odvětví j za totéž období a hodnota cj je vyrobené množství výrobku j odvětvím, které bylo dodáno do nevýrobní sféry nebo ponecháno pro vlastní zásoby.
(2.13) Odvětví /Výrobky
| 1 | 2 | ... | j | ... | n | |
| 1 | a11 | a12 | ... | a1j | ... | a1n |
| 2 | a21 | a22 | ... | a2j | ... | a2n |
| ... | ... | ... | ... | ... | ... | ... |
| i | ai1 | ai2 | ... | aij | ... | ain |
| ... | ... | ... | ... | ... | ... | ... |
| n | an1 | an2 | ... | anj | ... | ann |
| Výroba | V1 | V2 | ... | Vj | ... | Vn |
| Spotřeba | c1 | c2 | ... | cj | ... | cn |
Výměnnou charakteristikou tabulky je hodnota
Vi - ci,
pro kterou musí platit následující vztah
(2.14) ![]() aij
= Vi - ci
aij
= Vi - ci
1<=j<=n
Jestliže nyní vydělíme všechny prvky obecně j-tého sloupce hodnotou Vj , pak tyto podíly, označené jako 0aij můžeme chápat jako nezbytný objem výroby i-tého odvětví pro výrobu jednotky produkce odvětví j a hodnotu 0cj jako část produkce j-tého odvětví, spotřebovaná z jednotky produkce na nevýrobní účely.
Tato čísla v určitém smyslu mohou plně charakterizovat danou výrobní technologii a nazývají se koeficienty přímých spotřeb odvětví. Matice A koeficientů 0aij obsahuje dostatečně bohatou informaci o struktuře meziodvětvových vztahů, o existující technologii výroby. Tento model je plně použitelný i pro vztahy mezi dílnami a provozy závodu nebo firmy. Velmi užitečným se tento model jeví v oblastech dlouhodobého a krátkodobého plánování a prognózování výroby. Učiníme nyní dva závažné předpoklady:
1.Existující technologii v období (T0,T) považujeme za neměnnou.
2.Výrobní technologie je lineární.
Druhý předpoklad znamená,že pro výrobu xj jednotek se musí spotřebovat aij*xj jednotek výrobků každého odvětví i. Je zcela zřejmé, že jde o idealizaci, která by nás mohla dovést až k myšlence, že pokud budeme mít neomezené množství surovin, budeme moci vyrobit neomezené množství výrobků, což je pochopitelně nesmysl. Ve skutečnosti jsou výrobní možnosti omezeny jak technologií, tak i možnostmi a objemem základních fondů.
Předpokládejme, že za periodu T0,T budou všechna odvětví pracovat tak, že odvětví s pořadovým číslem j vyrobí xj jednotek. Označme jako vektor x vektor výroby. V takovém případě můžeme spočítat, jakou část celkové výroby spotřebujeme k jeho vytvoření. Použijeme-li maticová označení, pak můžeme vektor přímé spotřeby zadat jako součin
A .x
Zbytek, který můžeme použít jako spotřebu pro nevýrobní sféru, můžeme vyjádřit jako
c = x - A .x
Základní otázka, která vzniká při plánování výroby je tato : "Pro zadaný vektor c spotřeby určete nezbytnou velikost výroby."
Matematicky je třeba vlastně řešit rovnici:
(2.15) x - A .x = c
Takto zformulovaný model se nazývá modelem meziodvětvové výměny W.Leontiefa. Zase zůstává v platnosti to, co jsme říkali již dříve - obecný model meziodvětvové výměny je ve skutečnosti daleko bohatší, spočívá především v hlubší analýze vektoru c na jednotlivé složky, jako je akumulace, osobní spotřeba atd.
Ve výše uvedeném modelu předpokládáme mimo jiné okamžitou výrobu všech složek vektoru x. Pro modelování zpožděné výroby se matice A rozbíjí na bloky. Jestliže využijeme plánování na více period, pak můžeme řešit úlohu o maximálním zisku v ekonomice.
Nechť c=(c1,c2,...,cn) je vektor cen jednotlivých výrobků. Pak můžeme zformulovat následující úlohu:
(2.16) m a x ( c , xT)
A .xt+1 <= xt : t = 0,1,2,...,T-1
xt >= 0
Nehledě na řadu předností má tento model i celou řadu nedostatků. Například neakceptuje infrastrukturu společenské výroby ,třeba dopravu, přesto se ukazuje, že kvalitativní výsledky získané výzkumem tohoto modelu se při přechodu ke složitějším modelům mění jen málo.
Zobecníme model Leontiefa na případ, kdy jeden výrobek vyrábějí různá odvětví. Stejně jako v předchozím modelu budeme předpokládat,že v našem modelu existuje n různých druhů výrobků. Existuje však ještě m ( m >= n ) technologických procesů, z nichž každý vyrábí jeden výrobek. Obecně předpokládáme, že množina indexů M = {1,2,...,m} se rozpadá na disjunktní podmnožiny, které označíme MK .
Předpokládáme, že proces s číslem j E MK realizuje výrobu k-tého výrobku. Definujme dále incidenční matici I typu (m,n) jejímiž prvky jsou nuly a jedničky, podle následujícího pravidla
(2.17) I = ( eij) : eij = 0 , not j ![]() MK
MK
1 , j ![]() MK
MK
Jestliže vektor spotřeby označíme jako dříve, pak rovnice analogická rovnici (2.15) bude mít tvar
(2.18) I .x - A .x = c
Předpokládejme,že model Leontiefa je produktivní, jinými slovy, že rovnice 2.18 má nezáporná řešení pro každý konečný vektor spotřeby c. Předpokládejme, že každému technologickému procesu odpovídá koeficient spotřeby pracovní síly l. V takovém případě můžeme sestavit úlohu:
(2.19) m i n ( l , x )
( I - A ) .x = c , x >= 0
Jako zajímavý fakt je možno uvést,že tato úloha má tu vlastnost, že není nikdy třeba využívat všech m procesů. Existuje takových n procesů, že na nich má úloha 2.19 optimální řešení. Důkaz tohoto faktu vyplyne jako důsledek zvláštnosti řešení simplexové metody.
Pochopitelně existují i jiné než lineární modely, jak si ukážeme dále.
Tato úloha je tradiční matematickou úlohou. Je zadána funkce jedné proměnné f(t) na uzavřeném intervalu [0,1]. Tuto funkci chceme na tomto intervalu "co nejlépe" nahradit polynomem Pn(t) stupně n. V tomto případě aktivním prostředkem je výběr stupně polynomu a naší strategií výběr jeho koeficientů. Samotný cíl operace není přesně konkretizován, protože pod pojmem "co nejlépe " je možné si představit cokoliv. Proto je možné obecně zformulovat celou řadu kriterií:
(2.20)
W = - ![]() f(t)-Pn(t)
dt
f(t)-Pn(t)
dt
0
(2.21)
W = - m a x f(t) - Pn(t)
0<=t<=1
apod.
Tyto kriteria je nutné minimalizovat.
2.8. Optimální rozmístění zařízení kuchyně.
Tato úloha je vhodná pro začínající manželské páry. Spočívá v tom, že máme zatím prázdnou kuchyni a v ní m volných míst, na která je třeba umístit m kusů kuchyňského nábytku. Nechť půdorys kuchyně vypadá např. následovně:

Dalšími potřebnými údaji jsou dij ,což je vzdálenost mezi místy i a j a fkl, což je frekvence přechodů mezi věcí k a věcí l. Cílem operace je rozmístit věci na jednotlivá místa tak, aby se hospodyňka v nové domácnosti nachodila co nejméně.
Důležitou roli ve formulaci problému hraje výběr proměnných. V tomto případě zavedeme následující proměnné:
xik = 1 , jestliže je věc k umístěna na místě i
0 , v opačném případě
Při takovém zadání proměnných můžeme zformulovat cíl operace následujícím způsobem:
(2.22) m i n {![]()
![]()
![]()
![]() dij .fkl .xik .xjl}
dij .fkl .xik .xjl}
i j k l
Tento vztah znamená, že frekvenci krát vzdálenost mezi místy i,j a věcmi k,l bereme pouze v případě, kdy je věc k umístěna na místě i a věc l na místě j.
Pokud bychom již dále nic nepožadovali, bylo by řešení triviální. Optimální by bylo všechny věci umístit prostě na jednu hromadu s nulovou vzdáleností mezi sebou. Tak by se ovšem v kuchyni pracovat nedalo. Musíme tedy taková nesmyslná řešení odstranit. Budeme požadovat, aby každá věc byla umístěna právě na jednom místě a aby na každém místě byla umístěna právě jedna věc. Matematicky se tyto požadavky zapíší následovně:
(2.23) ![]() xik
= 1
xik
= 1 ![]() xik
= 1
xik
= 1
i k
Vztahy 2.22 a 2.23 spolu se zadáním proměnné x tvoří matematický model této úlohy. Cílová funkce (kriterium optimality nebo cíl operace) je v tomto případě kvadratickou funkcí.
Je zadáno N útočných prostředků jedné ze znepřátelených stran a M obranných prostředků druhé strany. Dále existuje k možných míst průlomu útočníkem obranou protivníka. Označme písmenem i čísla těchto míst.
Předpokládejme dále, že umístění jednoho obranného prostředku do místa možného průlomu i může zničit pi útočných prostředků protivníka. Cílem útočící strany je převést přes obranu co nejvíce svých prostředků, zatímco cílem obrany je pravý opak. Takovouto situaci nazýváme antagonistickou. Matematicky můžeme cíl agresora vyjádřit následovně
(2.24) m a x m i n ![]() m
a x {xi - pi .yi ; 0 }
m
a x {xi - pi .yi ; 0 }
x y i
kde x je vektor rozmístění prostředků útočníka a y je vektor rozmístění prostředků obrany.
Mimo to musí být splněny následující podmínky pro vektory x a y:
(2.25) xi,yi>=0 , ![]() xi
<= N ,
xi
<= N , ![]() yi
<= M
yi
<= M
Ve vztahu 2.24 se vyskytuje posloupnost max,min proto, že předpokládáme, že útočník nezná rozmístění prostředků obrany. V případě, že by toto rozmístění znal, byla by posloupnost min max.
Úloha: Dokažte, že pro každou spojitou funkci f(x,y) vektorových argumentů x,y na libovolném definičním oboru platí:
(2.26) m a x m i n f(x,y) <= m i n m a x f(x,y)
x y y x
Předpokládejme,že existuje n druhů výrobků, které jsou očíslovány indexy i a mohou být na trhu prodávány za ceny pi za jednotku zboží. Trh je přirozeně omezen jak poptávkou po množství ki produkce i-tého druhu, které může být řekněme za rok spotřebováno, tak i množstvím peněz na trhu C, které mohou být k nákupu zboží použity. Výrobu tvoří vektor x , jehož komponentami jsou množství vyráběných výrobků jednotlivých druhů. Předpokládejme dále, že existuje m výrobních prostředků gj(x), které mohou být spotřebovány výrobou. Celkové množství těchto prostředků je Vj.
Mimo to budeme předpokládat, že na trhu existuje konkurence, která může vyrábět množství yi a prodávat ho za ceny ri.
V takové situaci může být cílem operace maximalizace hrubého zisku z prodeje výrobků:
(2.27) max min {![]() pi.min(xi,ki-0yi);max(C -
pi.min(xi,ki-0yi);max(C - ![]() ri.0yi;0)}-gl(x)
ri.0yi;0)}-gl(x)
x y i i
kde
0yj = min ( ki; yi.max{(pi-ri)/ ri-pi ;0})
i
Přitom musí být splněny podmínky
(2.28) gj ( x ) <= Vj
Indexem l ve vztahu 2.27 jsme označili zvláštní druh výrobních prostředků - peníze.
Představme si, že je zadán určitý systém vzájemně propojených elementů (např. výrobní linka, radiolokační systém apod.). Systém se skládá z n prvků, které označíme čísly i a které se mohou nacházet právě v jednom ze dvou stavů :funguje nebo nefunguje. Předpokládejme dále, že tyto prvky jsou zapojeny seriově (za sebou). V tomto případě funkční porucha jediného článku soustavy vyvolá havárii celého systému.
Označme ti čas ukončení bezporuchové činnosti i-tého prvku systému. V takových označeních kriteriem efektivnosti celého systému bude následující funkce:
(2.29) W(t) = 1 , t <= m i n ( ti)
1<=i<=n
0 , v ostatních případech
Často se však jako samotné kriterium využívá i sama doba správné funkce systému, to znamená:
(2.30) T = m i n ti
1<=i<=n
Jako metodu zvýšení spolehlivosti systému lze použít např. metodu dublování jednotlivých prvků systému. Pokud se rozhodneme pro dublování prvků s čísly 1,2,...,m , pak získáme následující kriterium efektivnosti soustavy:
(2.31) W(t) = 1 , t <= m a x m i n ( tij)
1<=j<=m 1<=i<=n
0 , v ostatních případech
Obvykle však veličiny tij pro jednotlivé prvky systému nejsou přesně známy, někdy je však možné vyjádřit pravděpodobnost správné funkce daného prvku pij(t) a takovým způsobem vyjádřit střední hodnotu bezporuchové práce jednotlivého prvku jako
I
tij =![]() pij(t) dt
pij(t) dt
0
Obyčejně očekáváme, že pij(t) = exp(-t/tij), pokud tomu tak není, pak tij a disperse času
I
Dij = 2 .![]() t
.pij(t) dt - tij2
t
.pij(t) dt - tij2
0
neurčují jednoznačně pij .V takovém případě vzniká přirozená neurčitost.
Představme si, že na stavbu mají přivézt betonářskou ocel v čtyřmetrových prutech. Dále je známo, že pro betonáž je třeba 640 kusů ocelových prutů o délce 70 cm, 500 kusů o délce 130 cm a 200 kusů prutů o délce 260 cm. Cíle operace mohou být různe. Vyberme si dva cíle:
1. Kolik kusů prutů o délce čtyř metrů budeme minimálně potřebovat?
2. Kolik prutů budeme potřebovat, aby zbytky po odřezání prutů měly minimální souhrnnou délku?
Důležitým momentem je určení proměnné. V tomto případě je nejvhodnější za proměnnou považovat počet prutů řezaných určitým způsobem. Abychom mohli takové proměnné zavést, musíme nejprve určit možné způsoby řezání tyčí.
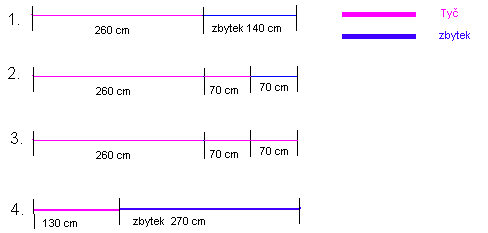
.............................................
atd.
Počet tyčí dělených daným způsobem i označíme jako xi. V takovém případě můžeme první cíl zformulovat matematicky jako:
(2.32) m i n {x1 + x2 + ...+ xn }
a druhý cíl jako
(2.33) m i n {140.x1 + 70.x2 + 0.x3 + 270.x4 + ...+ a.xn}
Omezující podmínky jsou pro obě úlohy stejné a vypadají následovně:
x1 + x2 + x3 = 200
x4 + 2.x5 + ...= 500
.....................
Ačkoliv obě úlohy mají stejné omezující podmínky, jejich řešení budou obecně různá!!! Závěr, který z toho plyne, je jasný - při formulaci problému a tvorbě matematického modelu musíme dávat bedlivý pozor na to, co skutečně chceme optimalizovat, protože i na první pohled podobně vypadající úlohy mohou mít podstatně rozdílná řešení.