m a x {![]() ai .ui
-
ai .ui
- ![]() bj
.vj }
bj
.vj }
4.2.3. Metoda potenciálů pro řešení dopravní úlohy.
Metoda, se kterou se nyní seznámíme, je zjednodušenou simplexovou metodou. Nejprve se budeme zabývat nedegenerovanou dopravní úlohou. Vytvoříme duální úlohu k dopravní úloze. První skupině omezujících podmínek přiřadíme vektor proměnných u a druhé skupině podmínek vektor proměnných -v. Jelikož samotná dopravní úloha je úlohou kanonickou, nebudeme po duálních proměnných požadovat nezápornost. Označení duálních proměnných u,-v je historické a nemá žádný hlubší smysl.
Duální úloha bude mít tedy tvar:
m a x {![]() ai .ui
-
ai .ui
- ![]() bj
.vj }
bj
.vj }
i j
ui - vj <= cij i=1,2,...,n j=1,2,...,m
Předpokládejme, že známe výchozí bazické řešení. Pak podle věty o stabilitě bude plán x=(xij) optimálním, právě když současně duální plán bude vyhovovat požadavku :
je-li xij>0 ,pak ui - vj = cij
Předpokládejme, že známe výchozí plán a jemu odpovídající bázi. Můžeme sestavit soustavu m+n-1 rovnic pro m+n neznámých a tuto soustavu vyřešit. Tím najdeme hodnoty duálních proměnných. Pokud je bazické řešení nedegenerované, má soustava vždy nekonečně mnoho řešení a jednu z proměnných můžeme volit libovolně. Potom prověříme splnění podmínek duální úlohy. Pokud jsou podmínky splněny, je nalezené bazické řešení současně optimální. Jestliže tomu tak není, je třeba přejít k jinému bazickému řešení. Do báze zavádíme tu proměnnou xij,
u které se nejvíce porušuje podmínka optimálnosti (nemůže to být proměnná s xij>0, neboť ta splňovala podmínku jako rovnost). Hodnotu této proměnné je tedy třeba změnit na nenulovou. V tabulce je možné realizovat přesun hodnot ve sloupcích a řádcích tak, aby součty zůstaly zachovány.
Celý postup přesunu je vhodné provádět na základě teorie grafů. Pokud označíme dodavatele a odběratele jako vrcholy grafu, pak nenulová přesunovaná množství můžeme označit jako spojnice odpovídajících vrcholů.
Platí, že bazickému řešení odpovídá graf, který je stromem. Máme-li do báze zařadit další vektor, t.j. další spojnici, znamená to, že do stromu doplníme jednu hranu a vznikne graf s jedním cyklem. Doplněná hrana má prozatím nulovou hodnotu přesunu. Přepravované množství přemístíme po tomto cyklu tak, že na doplněné hraně musí přibýt jistá hodnota, na další ubýt, na další zase přibýt atd. Stačí, když vybereme minimum z těch množství, ze kterých něco chceme brát a toto množství můžeme bez nebezpečí přesunout. Na místě minima vznikne nulový přesun a příslušnou hranu můžeme z grafu odstranit. Získáme opět strom, který odpovídá novému bazickému řešení.
Nyní se můžeme vrátit zpět k výpočtu nových hodnot duálních proměnných a ke kontrole optimálnosti řešení a celý postup opakujeme, dokud nezískáme optimální řešení. Celý výpočet organizujeme v tabulce. Pro názornost využijeme náš známý příklad a indexovou metodu (, aby bylo co řešit).
|
|
|
|
6 | ||||||||||||||||
|
|
|
|
8 | ||||||||||||||||
|
|
|
|
3 | ||||||||||||||||
|
|
|
|
9 | ||||||||||||||||
|
|
|
|
14 | ||||||||||||||||
| 10 | 18 | 7 | 5 | 40 |
Sestavíme soustavu rovnic pro duální proměnné (soustavu rovnic je možné řešit i přímo v tabulce)
u1 - v2 = 3 u1 - v4 = 1 u2 - v2 = 5
u3 - v1 = 1 u4 - v2 = 6 u4 - v3 = 10
u5 - v1 = 9 u5 - v2 = 9
Zobrazíme hodnoty duálních
proměnných do dalšího sloupce a
řádku,které
přidáme k tabulce.
|
|
|
|
6 | Duální proměnná U
3 |
||||||||||||||||
|
|
|
|
8 | 5 | ||||||||||||||||
|
|
|
|
3 | 1 | ||||||||||||||||
|
|
|
|
9 | 6 | ||||||||||||||||
|
|
|
|
14 | 9 | ||||||||||||||||
| 10 | 18 | 7 | 5 | 40 | |||||||||||||||||
| Proměnná V
0 |
0 | -4 | 2 |
V předchozí tabulce jsme uvedli tzv. duální ceny, jsou to hodnoty ui-vj a uvedeme je jako čísla psaná fialově v levém dolním rohu každého pole tabulky. U vyplněných polí je uvádět nebudeme, protože tam má toto číslo stejnou hodnotu jako normální sazba. Pole, ve kterých nejsou splněny podmínky optimálnosti jsou označeny jinou barvou pole (žlutou). Analogicky simplexové metodě vybíráme do báze tu hodnotu, u které je rozdíl přímé a duální sazby největší. Jedná se o pole (5,3). Sestavíme nyní odpovídající graf:
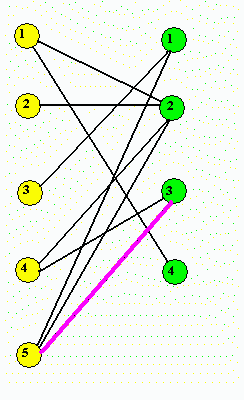
Nová hrana je doplněna čárkovanou čarou. Nyní je třeba najít cyklus v grafu. Jednoduchý algoritmus je následující: Najdeme všechny hrany, které končí v některém vrcholu grafu a odstraníme je. Tento postup opakuje tak dlouho, dokud jsou v grafu takové hrany. Výsledek tohoto postupu je na následujícím obrázku:
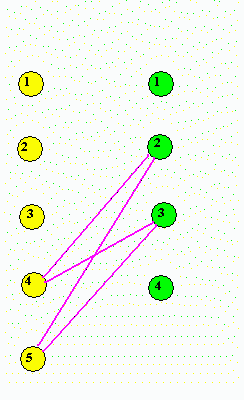
Na obrázku vidíme, které
hrany tvoří cyklus. Jedná se o doplněnou hranu
(5,3) a hrany (4,3), (4,2),(5,2). Na první uvedenou
máme přidat, z druhé
ubrat, na třetí přidat a ze čtvrté odebrat.
Vybereme tedy minimum z čísel
7,7 t.j. 7. Znázorníme si vybraný
cyklus v tabulce:
|
|
|
|
6 | Duální proměnná U
3 |
||||||||||||||||
|
|
|
|
8 | 5 | ||||||||||||||||
|
|
|
|
3 | 1 | ||||||||||||||||
|
|
|
|
9 | 6 | ||||||||||||||||
|
|
|
|
14 | 9 | ||||||||||||||||
| 10 | 18 | 7 | 5 | 40 | |||||||||||||||||
| Proměnná V
0 |
0 | -4 | 2 |
Přesuneme sedm jednotek tak, že od prvku (5,2) tuto hodnotu
odečteme,
k prvku (5,3) hodnotu 7 přičteme, od prvku (4,3) odečteme a k prvku
(4,2)
přičteme. Tímto postupem zůstane zachován součet
v řádcích i ve sloupcích
a vznikne nové bazické
řešení, protože minimálně jeden z
prvků (5,2) a
(4,3) se stane nulovým. V našem
případě bude řešení
degenerované (nulovými
se stanou dva prvky). Vytvoříme znovu soustavu rovnic,
která pro duální
proměnné odpovídá nenulovým
xij v tabulce. Problém je v tom, že soustava
bude obsahovat pouze m+n-2 rovnice a nebude snadno
řešitelná. Chybí nám
totiž jeden bazický vektor a do soustavy musíme
zahrnout i jednu nulovou
bazickou proměnnou. Nechť je to např. proměnná x43.
Situace po úpravě
a výpočtu duálních
proměnných je znázorněna v
následující tabulce.
|
|
|
|
6 | Duální proměnná U
3 |
||||||||||||||||
|
|
|
|
8 | 5 | ||||||||||||||||
|
|
|
|
3 | -4 | ||||||||||||||||
|
|
|
|
9 | 6 | ||||||||||||||||
|
|
|
|
14 | 4 | ||||||||||||||||
| 10 | 18 | 7 | 5 | 40 | |||||||||||||||||
| Proměnná V
-5 |
0 | -4 | 2 |
Řešení soustavy rovnic je rovněž v
tabulce a vypadá následovně:
u1 - v2 = 3 u1 - v4 = 1 u2 - v2 = 5
u3 - v1 = 1 u4 - v2 = 6 u4 - v3 = 10
u5 - v1 = 9 u5 - v3 = 8
V pravém dolním rohu jsou opět uvedeny
duální sazby. Nevyhovující
je pouze prvek (2,1). Sestrojit cyklus není již tak
jednoduché, jako bylo
v předešlém případě. Použijeme opět
metody teorie grafů.
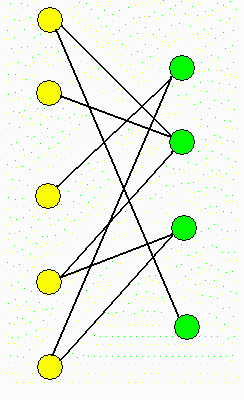
Výše uvedenou metodou odstraníme všechny hrany, které určitě netvoří cyklus a nový cyklus opět znázorníme v tabulce.
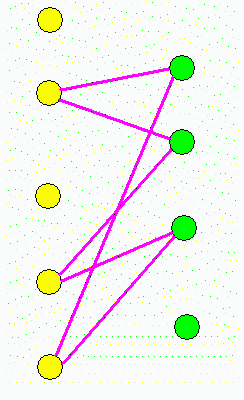
|
|
|
|
6 | ||||||||||||||||
|
|
|
|
8 | ||||||||||||||||
|
|
|
|
3 | ||||||||||||||||
|
|
|
|
9 | ||||||||||||||||
|
|
|
|
14 | ||||||||||||||||
| 10 | 18 | 7 | 5 | 40 |
Přesunovaná hodnota v tomto případě je nula!!!
Znamená to, že
prvek (4,3) z báze vyřadíme a zařadíme
prvek (2,1), změníme soustavu rovnic
a pokračujeme v řešení stejným
způsobem. Nakonec dojdeme k řešení,
které
je identické s řešením,
které jsme získali metodou VAM nebo metodou BAM.
Programová realizace
metody BAM a metody potenciálů.
PROGRAM DOPRAVNI_PROBLEM;
USES DOS;
LABEL 1,3,5,6,7;
CONST MAX1=50;MAX2=50;MAX3=100;
NIC=1E-4;
VAR A,U:ARRAY[1..MAX1] OF REAL;
V:ARRAY[1..MAX2] OF REAL;
NB,NE,IB,IE:ARRAY[1..MAX3] OF INTEGER;
C,D,X:ARRAY[1..MAX1,1..MAX2] OF REAL;
MIN,E1,E2,S1,S,DD,CAS:REAL;
II,JJ,I,J,M,N,M1,N1,K,L,Q,Q1,Q2,SS,KROK:INTEGER;
F,LST:TEXT;
HOD,MINU,SEC,MILISEC,HH,MM,SE,MILI:WORD;
SB,SB1:STRING[60];
PROCEDURE TISK;
LABEL 5;
VAR AS,BS:STRING[15];
BEGIN
WRITELN(LST);WRITELN(LST,'DODAVATEL ODBERATEL MNOZSTVI');
FOR I:=1 TO 30 DO WRITE(LST,'*');WRITELN(LST);
S:=0.0;
FOR I:=1 TO M1 DO FOR J:=1 TO N1 DO
BEGIN IF ROUND(X[I,J])=0 THEN GOTO 5;
WRITELN(LST,I:5,' ',J:9,ROUND(X[I,J]):6);
S:=S+ROUND(X[I,J])*D[I,J];
5:END;
FOR I:=1 TO 30 DO WRITE(LST,'*');WRITELN(LST);
WRITELN(LST,'HODNOTA NAKLADU NA PREPRAVU JE ',S:8:1)
END;
BEGIN
1WRITE('NAZEV SOUBORU VSTUPU :');READLN(SB);
WRITE('NAZEV SOUBORU VYSTUPU :');READLN(SB1);
ASSIGN(LST,SB1);REWRITE(LST);
ASSIGN(F,SB);(*$I-*) RESET(F);(*$I+*)
IF IORESULT<>0 THEN BEGIN WRITELN('SOUBOR NENALEZEN');EXIT END;
FOR I:=1 TO MAX1 DO FOR J:=1 TO MAX2 DO BEGIN C[I,J]:=0;D[I,J]:=0;
X[I,J]:=0 END;
READLN(F,M,N);
E1:=1/(5*M);S1:=0.0;S:=0.0;E2:=1/(7*N);
FOR I:=1 TO M DO
BEGIN READ(F,A[I]);A[I]:=A[I]+E1;S1:=S1+A[I] END;
READLN(F);
FOR I:=1 TO N DO
BEGIN READ(F,B[I]);B[I]:=B[I]-E2;S:=B[I]+S END;
READLN(F);M1:=M;N1:=N;
IF S<S1 THEN
BEGIN M1:=M;N1:=N;N:=N+1;B[N]:=S-S1 END;
IF S1<S THEN
BEGIN N1:=N;M1:=M;M:=M+1;A[M]:=S1-S END;
FOR I:=1 TO M1 DO
BEGIN FOR J:=1 TO N1 DO BEGIN READ(F,C[I,J]);D[I,J]:=C[I,J] END;
READLN(F)
END;
FOR I:=1 TO N DO FOR J:=1 TO M DO X[I,J]:=0;
GETTIME(HH,MM,SE,MILI);HOD:=HH;MINU:=MM;SEC:=SE;MILISEC:=MILI;
1:FOR I:=1 TO M DO IF ABS(A[I])>NIC THEN
BEGIN MIN:=1.0E30;
FOR J:=1 TO N DO
IF (ABS(B[J])>NIC) AND (MIN>C[I,J]) THEN MIN:=C[I,J];
FOR J:=1 TO N DO
IF ABS(B[J])>NIC THEN C[I,J]:=C[I,J]-MIN
END;
FOR J:=1 TO N DO IF ABS(B[J])>NIC THEN
BEGIN MIN:=1.0E30;
FOR I:=1 TO M DO
IF (ABS(A[I])>NIC) AND (MIN>C[I,J]) THEN MIN:=C[I,J];
FOR I:=1 TO M DO
IF ABS(A[I])>NIC THEN C[I,J]:=C[I,J]-MIN
END;
S1:=-1.0;
FOR I:=1 TO M DO IF ABS(A[I])>NIC THEN
FOR J:=1 TO N DO IF (ABS(B[J])>NIC) AND (ABS(C[I,J])<NIC) THEN
BEGIN MIN:=1.0E30;S:=0.0;
FOR K:=1 TO M DO
IF (K<>I) AND (ABS(A[K])>NIC) AND (MIN>C[K,J]) THEN MIN:=C[K,J];
IF MIN=1.0E30 THEN MIN:=0.0;
S:=S+MIN;MIN:=1.0E30;
FOR K:=1 TO N DO
IF (K<>J) AND (ABS(B[K])>NIC) AND (MIN>C[I,K]) THEN MIN:=C[I,K];
IF MIN=1.0E30 THEN MIN:=0.0;
S:=S+MIN;
IF S>=S1 THEN BEGIN
II:=I;JJ:=J;S1:=S END
END;
X[II,JJ]:=B[JJ];
IF A[II]<B[JJ] THEN X[II,JJ]:=A[II];
A[II]:=A[II]-X[II,JJ];B[JJ]:=B[JJ]-X[II,JJ];
FOR I:=1 TO N DO IF ABS(B[I])>NIC THEN GOTO 1;
GETTIME(HH,MM,SE,MILI);
WRITELN(LST,'BAZOVE RESENI');WRITELN(LST);
TISK;
WRITELN(LST,'DOBA VYPOCTU BAZICKEHO RESENI:',SE-SEC+60*(MM-MINU+60*(HH-HOD )));
HOD:=HH;MINU:=MM;SEC:=SE;MILISEC:=MILI;WRITELN(LST);
WRITELN(LST,'OPTIMALNI RESENI');KROK:=0;
REPEAT L:=1;
FOR I:=1 TO M DO FOR J:=1 TO N DO IF ABS(X[I,J])>NIC THEN
BEGIN NB[L]:=I;NE[L]:=J;IB[L]:=0;IE[L]:=0;L:=L+1 END;
II:=NB[1];U[II]:=0;IB[II]:=1;
REPEAT S:=1;
FOR I:=1 TO L-1 DO
BEGIN II:=NB[I];JJ:=NE[I];
IF (IB[I]=0) AND (IE[I]=1) THEN
BEGIN S:=0;IB[I]:=1;
U[II]:=D[II,JJ]+V[JJ];
END;
IF (IB[I]=1) AND (IE[I]=0) THEN
BEGIN S:=0;IE[I]:=1;
V[JJ]:=U[II]-D[II,JJ]
END;
IF (IB[I]=1) AND (IE[I]=1) THEN
FOR K:=1 TO L-1 DO
BEGIN IF NB[K]=II THEN IB[K]:=1;
IF NE[K]=JJ THEN IE[K]:=1
END
END
UNTIL S=1;
DD:=0;
FOR I:=1 TO M DO FOR J:=1 TO N DO
BEGIN S:=U[I]-V[J]-D[I,J];
IF S>DD THEN BEGIN DD:=S;II:=I;JJ:=J END
END;
IF DD<0.01 THEN BEGIN GETTIME(HH,MM,SE,MILI);TISK;
WRITELN(LST,'POCET KROKU OPTIMALIZACE : ',KROK:5);
WRITELN(LST,'DOBA OPTIMALIZACE :',SE-SEC+60*(MM-MINU+60*(HH-HOD))+(
HOD:=HH;MINU:=MM;SEC:=SE;MILISEC:=MILI;WRITELN(LST);CLOSE(LST);EXIT;
{VYCHOD Z PROGRAMU }KROK:=KROK+1;
NB[L]:=II;NE[L]:=JJ;IB[L]:=0;IE[L]:=0;
REPEAT DD:=0;
FOR I:=1 TO L DO
BEGIN Q1:=0;Q2:=0;
S:=NB[I];S1:=NE[I];
IF (S>=0) OR (S1>=0) THEN
BEGIN FOR J:=1 TO L DO IF I<>J THEN
BEGIN IF S=NB[J] THEN Q1:=1;
IF S1=NE[J] THEN Q2:=1
END;
IF (Q1+Q2)<2 THEN
BEGIN NB[I]:=-1;NE[I]:=-1;DD:=1 END
END
END
UNTIL DD=0;
SS:=II;Q:=JJ;MIN:=MAXINT;
3:I:=1;
WHILE ((SS=NB[I]) OR (Q<>NE[I])) AND (I<=L) DO I:=I+1;
IF I<=L THEN
BEGIN SS:=NB[I];
IF MIN>X[SS,Q] THEN MIN:=X[SS,Q];
IF SS=II THEN GOTO 5
END;
I:=1;
WHILE ((SS<>NB[I]) OR (Q=NE[I])) AND (I<=L) DO I:=I+1;
IF I<=L THEN
BEGIN Q:=NE[I];
IF Q<>JJ THEN GOTO 3
END;
5:SS:=II;Q:=JJ;
6:I:=1;
WHILE ((SS=NB[I]) OR (Q<>NE[I])) AND (I<=L) DO I:=I+1;
IF I<=L THEN
BEGIN SS:=NB[I];X[SS,Q]:=X[SS,Q]-MIN;
IF SS=II THEN GOTO 7
END;
I:=1;
WHILE ((SS<>NB[I]) OR (Q=NE[I])) AND (I<=L) DO I:=I+1;
IF I<=L THEN
BEGIN Q:=NE[I];X[SS,Q]:=X[SS,Q]+MIN;
IF Q<>JJ THEN GOTO 6
END;
7:X[II,JJ]:=MIN;
UNTIL 1>2
END.
FORMÁT VSTUPNÍCH DAT. VÝSTUPNÍ SESTAVA
4 4 .....................................BAZOVE RESENI
117 37 51 60
156 54 50 5 ....................DODAVATEL ODBERATEL MNOZSTVI
******************************
12 9 5 7 .........................1 1 17
14 7 3 5 ........................2 1 37
18 1 1 3 ........................3 3 46
9 3 5 9 ..........................3 4 5
4 1 2
4 2 54
4 3 4
******************************
HODNOTA NAKLADU NA PREPRAVU JE 443.0
DOBA VYPOCTU BAZICKEHO RESENI : .11 SEKUND
OPTIMALNI RESENI
DODAVATEL ODBERATEL MNOZSTVI
******************************
1 1 17
2 1 37
3 3 46
3 4 5
4 1 2
4 2 54
4 3 4
******************************
HODNOTA NAKLADU NA PREPRAVU JE 443.0
POCET KROKU OPTIMALIZACE : 0
DOBA OPTIMALIZACE : 0.06 SEKUND
V uvedeném programu je využito zajímavé metody, která umožňuje zaručit nedegenerovanost problému, pokud jsou hodnoty úlohy celočíselné. Jedná se o metodu malého parametru. K jednotlivým hodnotám ai a bj se přičtou nebo odečtou určitá malá necelá čísla .Díky tomu nemůže nastat degenerace úlohy a po vyřešení problému se zpětně výsledky zaokrouhlí.
Upozorněme ještě na jednu zvláštní vlastnost metody řešení dopravní úlohy. Pokud jsou výchozí údaje celočíselné, jsou všechna bazická řešení celočíselná a celočíselné je i optimální řešení.
Přejděme nyní k jiné třídě
úloh a právě k celočíselným
úlohám. Budeme
i nadále předpokládat, že
omezující podmínky a
cílová funkce jsou lineární.
Metody řešení úloh lineárního programování, se kterými jsme se zatím seznámili, předpokládaly, že se proměnné mohou měnit spojitě.
Existuje však celá řada úloh, kdy tomu tak není. Jsou to úlohy o výrobním plánu s kusovými výrobky a některé další speciální úlohy.
Úloha o batohu.
Turista stojí před následujícím problémem. Má si vzít na expedici určité vybavení a stojí před obrovskou hromadou věcí. Je zřejmé, že všechny se do jeho batohu nevejdou. Nesmí překročit určitou váhu, jinak by batoh neunesl a nesmí překročit ani určitý objem, protože jinak by mu batoh praskl. Každá věc je charakterizována svojí váhou a svým objemem. Předpokládejme, že turista umí ocenit hodnotu jednotlivých věcí, které chce vzít s sebou. Jinou hodnotu má asi kus chleba a jinou hodnotu mají sebrané spisy. Matematický model úlohy by mohl být následující:
m a x {( c, x )}
A.x < b , x > 0 , x - je vektor celých čísel.
Vidíme, že úloha se liší od úloh lineárního programování pouze podmínkou celočíselnosti.
Úloha o optimálním přiřazení.
Řekněme, že určitý stavební podnik má na n stavbách n míchaček a chce je přemístit na n jiných staveb. Jsou známy náklady na přepravu mezi jednotlivými místy. Cílem operace je přemístit míchačky z jedněch staveb na druhé tak, aby náklady na přepravu byly minimální. Matematický model operace je tento:
m i n ![]()
![]() cij .xij
cij .xij
![]() xij
= 1 ,
xij
= 1 ,![]() xij = 1 ,
xij = 1 ,
xij je 0 nebo 1 (0<xij< 1, xij- celé číslo)
Tato úloha připomíná dopravní problém a díky tomu, co jsme si řekli na konci minulého paragrafu ji můžeme vyřešit pomocí metody potenciálů. Problémem je však absolutní degenerovanost úlohy. Tato úloha má ještě speciálnější tvar než dopravní úloha a existuje daleko efektivnější způsob, jak ji vyřešit.
O metodě řešení tohoto problému se dovíme v dalším paragrafu.
Úloha o obchodním cestujícím.
S touto úlohou jsme se již setkali v metodě Littla, a proto ji nebudeme znovu formulovat. Napíšeme pouze její matematický model z oblasti lineárního programování:
m i n ![]()
![]() cij.xij
cij.xij
![]() xij
= 1 ,
xij
= 1 , ![]() xij
= 1,
xij
= 1,
vi - vj + n.xij < n-1
xij je 0 nebo 1 (0<xij< 1, xij- celé číslo)
Podmínku celočíselnosti je možné matematicky formulovat snadno, ale dostaneme se za rámec lineárního programování, takže si práci neusnadníme, právě naopak.Např.
s i n( p .x) = 0.
Druhou možností je tzv."inženýrský" přístup. Jedná se o následující postup: Vyřešíme úlohu nejprve bez ohledu na podmínku celočíselnosti a řešení prostě zaokrouhlíme.
Následující příklad názorně ukazuje nesmyslnost tohoto způsobu řešení v obecném případě. Neznamená to ale, že je tento postup vždy nepřijatelný.
Příklad.
Mějme úlohu
m a x {x1 - 3*x2 + 3*x3 }
-3*x1 + 2*x2 + x3 < =3
4 *x1 - 3*x2 < =2
2 *x1 + x2 - x3 < =4, x >= 0
x - je vektor celých čísel
Pokud vyřešíme tuto úlohu bez ohledu na celočíselnost simplexovou metodou získáme následující řešení: (0.5 ; 0 ; 4.5 ). Zaokrouhlením můžeme získat tato řešení: ( 0 ; 0 ; 4); ( 0 ; 0 ; 5 );( 1 ; 0 ; 4);( 1 ; 0 ; 5);
Dosazením do jednotlivých omezujících podmínek úlohy se můžeme přesvědčit, že ani jedno z těchto řešení není nejen optimální, ale dokonce není ani přípustným plánem této úlohy !!!
Pro řešení úlohy o optimálním přiřazení můžeme použít postup,který jsme využili již v algoritmu Littla i v dopravní úloze. Úlohu zpřehledníme tím, že provedeme redukci matice sazeb. Od řádků a pak od sloupců odečteme vždy minimální sazbu z řádku a sloupce. Matice se stane přehlednější a navíc součet všech odečtených prvků dá určitý odhad minima cílové funkce. Kdyby nastala taková situace, že by se nám podařilo vybrat n nulových prvků matice sazeb tak, že každý z těchto prvků by byl právě jeden ve sloupci a právě jeden v řádku, pak bychom měli optimální řešení, protože hodnota cílové funkce by byla rovna hodnotě minoranty. Pokud se nám nepodaří vybrat tímto způsobem potřebný počet prvků (nul), získáme řešení, které není přípustné a musíme se ho snažit zlepšit (což se projeví pochopitelně nárůstem cílové funkce). Nulové sazby, které označíme tak, že v řádku a sloupci je nejvýše jedna taková nula, budeme nazývat nezávislé. Platí následující důležitá věta:
Věta 4.3.1.1 (Königova věta)
Maximální počet nulových prvků v matici sazeb, které neleží současně v jednom řádku nebo sloupci, je roven minimálnímu počtu čar, kterými lze po řádcích nebo sloupcích pokrýt všechny nuly matice.
Důkaz
Dejme tomu, že počet krycích čar je roven "t" a skládá se z "r" vyškrtnutých řádků a "s" vyškrtnutých sloupců. Je zřejmé, že počet nezávislých nul nemůže být větší než "t", protože v každém sloupci a řádku může být pouze jedna taková nula. Z druhé strany všechny nezávislé nuly, které se nenacházejí v "r" vyškrtnutých řádcích, musí nutně ležet v "t" vyškrtnutých sloupcích, jinak by bylo možné pokrýt všechny nuly nižším počtem čar. Tím je věta dokázána.
Algoritmus metody.
KROK 1. Provedeme redukci matice sazeb.
KROK 2. Vybereme maximální počet nezávislých nul a odpovídajícím proměnným přiřadíme hodnotu xij = 1. Pokud jsme označili n takových nul, získali jsme optimální řešení a algoritmus je ukončen.
KROK 3. Pokryjeme všechny nuly matice minimálním počtem čar (viz. Königova věta). V matici musí zůstat neprázdná nepokrytá submatice. V této submatici vybereme nejmenší sazbu a tuto sazbu odečteme od nepokrytých sloupců a přičteme k pokrytým sloupcům. Prvky, které jsou přeškrtnuty jednou, se nemění, prvky přeškrtnuté dvakrát se o tuto sazbu zvětší a nepřeškrtnuté prvky se o tuto sazbu sníží.
Vrátíme se ke kroku 2. algoritmu.
Algoritmus označení nezávislých nul.
1. Vybereme řádek (sloupec), který obsahuje minimální počet nul.
2. V tomto řádku (slouci) označíme nulu tak, aby ji obsahující sloupec (řádek)
obsahoval minimální počet nul, je-li takových víc, vybereme první.
3. Takto vybraný řádek a sloupec vyškrtneme a vrátíme se k prvnímu kroku
algoritmu.
4. Proces je ukončen, když matice neobsahuje již žádný prvek.
Algoritmus výběru minimálního pokrytí nul.
1. Vybereme řádek (sloupec) obsahující maximální počet nul, pokud je takových
víc, vybereme první.
2. Vybraný řádek (sloupec) vyškrtneme.
3. Postup opakujeme tak dlouho, dokud v matici existují nevyškrtnuté nuly.
Doposud jsme se zabývali řešením minimalizačního problému. Maximalizační problém převedeme na minimalizační tak, že v matici sazeb vybereme maximální sazbu a od této sazby odečteme všechny sazby uvedené v matici. S touto novou maticí pak řešíme minimalizační úlohu.
Příklad.
Předpokládejme, že máme k dispozici tři výkonné stroje, které mohou pracovat na třech různých pracovištích. Protože se jedná o různé stroje a odlišné podmínky, budou stroje podávat na odlišných pracovištích odlišné výkony. Výkonnost strojů je uvedena v tabulce. Cílem operace je přiřadit stroje jednotlivým pracovištím tak, aby celkový výkon byl co nejvyšší.
| Pracoviště . / stroj | 1 | 2 | 3 |
| 1 | 62 | 54 | 56 |
| 2 | 67 | 65 | 53 |
| 3 | 29 | 18 | 35 |
Maximálním číslem v tabulce je číslo 67. Odečteme tedy od tohoto čísla všechny sazby tabulky
| Pracoviště . / stroj | 1 | 2 | 3 |
| 1 | 5 | 13 | 11 |
| 2 | 0 | 2 | 14 |
| 3 | 38 | 49 | 32 |
Provedeme redukci matice sazeb. Od každého řádku odečteme minimální prvek.
| Pracoviště . / stroj | 1 | 2 | 3 |
| 1 | 0 | 8 | 6 |
| 2 | 0 | 2 | 14 |
| 3 | 6 | 17 | 0 |
Od každého sloupce odečteme minimální prvek.
| Pracoviště . / stroj | 1 | 2 | 3 |
| 1 | 0 | 6 | 6 |
| 2 | 0 | 0 | 14 |
| 3 | 6 | 15 | 0 |
Vidíme, že v této tabulce je již optimální řešení a další kroky výpočtu nemusíme provádět. Optimální je umístit první stroj na první lokalitu, druhý na druhou a třetí na třetí.
Další příklad budeme orientovat pouze na metodu řešení již zadané a redukované matice sazeb.
Příklad.
| 0 | 0-1 | 0 | 0 |
| 0-1 | 2 | 4 | 6 |
| 0 | 4 | 6 | 8 |
| 0 | 8 | 16 | 24 |
V tomto případě můžeme označit pouze dvě nezávislé nuly a to libovolně v řádcích 2 - 4 a sloupcích 2 - 4. Všechny nuly lze podle Königovy věty pokrýt dvěma čarami. Tuto situaci znázorňuje následující obrázek:
| 2 | 0 | 0-1 | 0 |
| 0 | 0-1 | 2 | 4 |
| 0-1 | 2 | 4 | 6 |
| 0 | 6 | 14 | 22 |
Ve zbylé submatici je minimálním prvkem číslo 2. Odečteme tedy číslo dvě od nepokrytých řádků a přičteme je k pokrytým sloupcům. Po tomto kroku vznikne následující matice:
| 4 | 0 | 0-1 | 0 |
| 2 | 0-1 | 2 | 4 |
| 0-1 | 0 | 2 | 4 |
| 0 | 4 | 12 | 20 |
V nové matici je možné označit tři nezávislé nuly a i počet krycích čar musí tomuto počtu odpovídat:
| 4 | 2 | 0 | 0-1 |
| 2 | 0 | 0-1 | 2 |
| 0 | 0-1 | 0 | 2 |
| 0-1 | 4 | 10 | 18 |
V poslední matici je již obsaženo optimální řešení úlohy.
Cvičení.
Řešte následující
úlohy na optimální
přiřazení:
1 02 03 004
2 04 08 016
3 09 27 091
4 16 64 126
50 35 36 44 40
46 48 40 42 28
40 32 36 34 38
38 29 30 32 32
42 36 32 34 30
Metoda odsečení pro celočíselné úlohy.
Budeme se zabývat kanonickou úlohou lineárního programování s doplnitelnými celočíselnými omezeními na proměnné. Celkem logickým postupem řešení, který se nám nabízí, je následující postup. Vyřešme úlohu bez ohledu na podmínku celočíselnosti a pokud je řešení celočíselné, je i optimální. Pokud řešení není celočíselné, vybereme nějakou doplnitelnou podmínku, která by neomezila celočíselná řešení, ale naše konkrétní neceločíselné by vyloučila z množiny přípustných řešení úplně. Tuto novou úlohu můžeme dál řešit s novou podmínkou např. duálně simplexovou metodou. Proces je možné dále opakovat.
Základní otázka,
která zůstává, je otázka,
jak vytvářet tato nová omezení
(odsečení).
Definice 4.3.2.1
Nechť x* je neceločíselným optimálním plánem pro výchozí úlohu. Nerovnici ( , x ) < 0 nazveme regulárním odsečením, jestliže vyhovuje následujícím podmínkám:
1. Vektor x* nesplňuje tuto omezující podmínku.
2. Je-li x celočíselným plánem výchozí úlohy, pak tuto podmínku splňuje.
Gomoryho regulární odsečení.
Popíšeme nyní způsob sestavení regulárního odsečení, který navrhl Gomory. Pro libovolná reálná čísla ß zavedeme pojem celé části reálného čísla [ß], což je největší celé číslo, které je menší nebo rovno ß.
Příklad.
[2.315687] = 2 , [3.8569745] = 3 , [ - 1.75842] = -2
Dále zavedeme pojem necelá část reálného čísla {ß}, pro kterou platí
{ß} = ß - [ß]
Příklad.
{2.315687} = 0.315687 , {-1.75 }= 0.25 apod.
Všimněme si zejména toho, že necelá část je vždy nezáporné číslo.
Předpokládejme, že jsme vyřešili úlohu lineárního programování bez ohledu na omezení celočíselnosti a získali jsme neceločíselné optimální řešení v simplexové tabulce. Pak existuje komponenta vektoru b , která není celočíselná. Sestavme k odpovídajícímu řádku simplexové tabulky následující výraz
si = - {bi }+ ![]() {aij
}* xij
{aij
}* xij
Zavedeme další bazickou proměnnou si a přidáme tento vztah jako další omezující podmínku. Je zřejmé, že pokud bylo řešení neceločíselné, nebude tuto podmínku splňovat. -{bi} je záporná hodnota a řešení není přípustným plánem. Pokud by řešení bylo celočíselné, podmínka bude splněna {bi} = 0. Nyní je možné provést krok duálně simplexové metody, protože řešení i po přidání této podmínky je pseudoplánem (důsledek původní optimálnosti řešení). Je zřejmé, že takto vyrobené odsečení je regulární.
Příklad.
Mějme zadánu následující úlohu lineárního programování
m a x {x1 + 2 * x2 }
-3 * x1 + 4 * x2 < 6
4 * x1 + 3 * x2 < 12 , x > 0 a
x![]() Z2.
Z2.
Převedeme úlohu na kanonický tvar a sestavíme simplexovou tabulku. V simplexové tabulce vyřešíme problém bez ohledu na podmínku celočíselnosti:
| b | x1 | x2 | x3 | x4 | |
| c | 0 | -1 | -2 | 0 | 0 |
| 6 | -3 | 4 | 1 | 0 | |
| 12 | 4 | 3 | 0 | 1 |
| b | x1 | x2 | x3 | x4 | |
| c | 3 | -2,5 | 0 | 0,5 | 0 |
| 1,5 | -0,75 | 1 | 0,25 | 0 | |
| 7,5 | 6,25 | 0 | -0,75 | 1 |
| b | x1 | x2 | x3 | x4 | |
| c | 6 | 0 | 0 | 0,2 | 0,40 |
| 2,4 | 0 | 1 | 0,16 | 0,12 | |
| 1,2 | 1 | 0 | -0,12 | 0,16 |
Získali jsme optimální řešení neceločíselné úlohy. Ani jedna z komponent řešení není celočíselná, a proto vybereme takovou, která má největší celočíselný zbytek (odpovídá druhému řádku tabulky). Sestavíme novou podmínku ( Gomoryho odsečení ) a přidáme ji nakonec simplexové tabulky:
| b | x1 | x2 | x3 | x4 | s1 | |
| c | 6 | 0 | 0 | 0,20 | 0,40 | 0 |
| 2,4 | 0 | 1 | 0,16 | 0,12 | 0 | |
| 1,2 | 1 | 0 | -0,12 | 0,16 | 0 | |
| s1 | -0,4 | 0 | 0 | -0,16 | -0,12 | 1 |
Provedeme krok duálně simplexovou metodou a získáme následující simplexovou tabulku:
| b | x1 | x2 | x3 | x4 | s1 | |
| c | 5,5 | 0 | 0 | 0 | 0,25 | 1,25 |
| x2 | 2 | 0 | 1 | 0 | 0 | 1 |
| x1 | 1,5 | 1 | 0 | 0 | 0,25 | -0,75 |
| x3 | 2,5 | 0 | 0 | 1 | 0,75 | -6,25 |
x1 není nadále celočíselnou hodnotou, proto přidáme novou omezující podmínku, kterou vytvoříme jako odsečení z třetího řádku tabulky a pokračujeme v řešení.
| b | x1 | x2 | x3 | x4 | s1 | s2 | |
| c | 5,5 | 0 | 0 | 0 | 0,25 | 1,25 | 0 |
| x2 | 2 | 0 | 1 | 0 | 0 | 1 | 0 |
| x1 | 1,5 | 1 | 0 | 0 | 0,25 | -0,75 | 0 |
| x3 | 2,5 | 0 | 0 | 1 | 0,75 | -6,25 | 0 |
| s2 | -0,5 | 0 | 0 | 0 | -0,25 | 0,75 | 1 |
Měl by ještě následovat jednotkový bazický sloupec vektoru s2, ale ten není podstatný, stejně jako není podstatný sloupec předešlé nové podmínky. Tyto vektory se do báze nikdy nevracejí. Další tabulka je již optimální.
| b | x1 | x2 | x3 | x4 | |
| c | 5 | 0 | 0 | 0 | 0 |
| x2 | 2 | 0 | 1 | 0 | 0 |
| x1 | 1 | 1 | 0 | 0 | 0 |
Při dodržení určitých pravidel si můžeme dovolit neudržovat v tabulce všechny vektory- sloupce, je jen třeba dát pozor, abychom nezavedli do báze dvakrát stejný vektor.
Gomoryho algoritmus dovoluje řešit i smíšené úlohy lineárního programování. V takových úlohách mohou být některé proměnné celočíselné a jiné se mohou měnit spojitě. V takovém případě se algoritmus změní pouze málo. Odsečení se vytváří pouze u řádků, jejichž proměnná musí být celočíselná.
Program pro jednoduchý výpočet simplexovou metodou.
program simplex;
LABEL 99,1;
CONST MI=1E10;MM=1E-4;
TYPE MAT= ARRAY[1..20,1..20] OF REAL;
VAR L,JL,I,J,K,IL,LL,M,N,NP:INTEGER;
A:MAT;V:SET OF 1..20;
MIN,S,MN:REAL;
PROCEDURE PIS(A:MAT;M,N:INTEGER);
VAR I,J:INTEGER;
BEGIN FOR I:=1 TO M DO BEGIN
FOR J:=1 TO N DO WRITE(A[I,J]:6:2);WRITELN END
END;
BEGIN WRITELN('ZADEJ DATA: M N NP L ');READLN(M,N,NP,L);
WRITELN('M= ',M:3,'N= ',N:3,'NP= ',NP:3,'L= ',L:3);
WRITELN;WRITELN('ZADEJ SIMPLEXOVOU TABULKU:');
FOR I:=1 TO M DO BEGIN
FOR J:=1 TO N DO READ(A[I,J]);READLN END;
WRITELN;
PIS(A,M,N);
IF L=0 THEN JL:=2 ELSE JL:=3;
WHILE JL-L>1 DO BEGIN
1:K:=2;MN:=A[L+1,2];FOR J:=3 TO N DO BEGIN
S:=A[L+1,J];IF S<MN THEN BEGIN MN:=S;K:=J
END END;
IF MM<-MN THEN BEGIN MIN:=MI;
FOR I:=JL TO M DO IF A[I,K]>MM THEN BEGIN S:=A[I,1]/A[I,K];
IF MIN>S THEN MIN:=S END;
V:=[];LL:=0;IL:=0;
FOR I:=JL TO M DO IF A[I,K]>MM THEN IF (MIN*A[I,K]>A[I,1]-MM)
AND (A[I,1]+MM>MIN*A[I,K]) THEN BEGIN V:=V+[I];LL:=LL+1;IL:=I
END;J:=3;
IF LL=0 THEN BEGIN WRITELN('FUNKCE NEOMEZENE ROSTE!!!');GOTO 99 END;
WHILE LL>1 DO BEGIN MIN:=MI;
FOR I:=JL TO M DO IF (I IN V) AND (MIN>A[I,J]) THEN MIN:=A[I,J];
FOR I:=JL TO M DO IF (I IN V) THEN IF (A[I,J]+MM>MIN) AND
(MIN >A[I,J]-MM) THEN BEGIN
V:=V-[I];LL:=LL-1 END ELSE IL:=I;J:=J+1 END;
WRITELN('ITERACE : ',IL,K);
MIN:=A[IL,K];
PIS(A,M,N);
FOR J:=1 TO N DO BEGIN S:=A[IL,J]/MIN;A[IL,J]:=S; END;
FOR I:=1 TO M DO BEGIN S:=A[I,K];
FOR J:=1 TO N DO IF NOT(IL=I) THEN A[I,J]:=A[I,J]-A[IL,J]*S END END;
IF (-MN)>MM THEN GOTO 1;
L:=L+1;N:=N-NP END;
IF (L=2) AND (JL=3) AND (A[1,1]<-MM) THEN BEGIN
WRITELN('ULOHA NEMA PRIPUSTNE RESENI!!!'); GOTO 99 END;
WRITELN('VYSLEDKY :');PIS (A,M,N);
99:WRITELN('KONEC VYPOCTU')
END.
Zadání vstupních dat:
3 6 0 0 -------------počet řádků tabulky,počet sloupců, počet pom.proměnných, 0 nebo 1 - řešit pomocnou úlohu nebo ne
0 -1 -1 -1 0 0 ----simplexová tabulka v obvyklé formě, pokud je pomocná účelová funkce, je prvním řádkem, druhým zadaná cílová funkce.
10 1 2 4 1 0
5 0 1 - 1 0 1
V zadání se jedná o úlohu:
m a x {x1 + x2 + x3 }
x1 + 2 * x2 + 4 * x3 < 10
x2 - x3 < 5 , x > 0
Výsledky programu:
0.00 -1.00 -1.00 -1.00 0.00 0.00
10.00 1.00 2.00 4.00 1.00 0.00
5.00 0.00 1.00 -1.00 0.00 1.00
ITERACE : 2 2
0.00 -1.00 -1.00 -1.00 0.00 0.00
10.00 1.00 2.00 4.00 1.00 0.00
5.00 0.00 1.00 -1.00 0.00 1.00
VYSLEDKY :
10.00 0.00 1.00 3.00 1.00 0.00
10.00 1.00 2.00 4.00 1.00 0.00
5.00 0.00 1.00 -1.00 0.00 1.00
KONEC VYPOCTU
Doposud jsme se zabývali řešením situací s lineárními omezujícími podmínkami a s lineární cílovou funkcí. Příroda kolem nás je však mnohotvárná a není žádný důvod předpokládat, že jevy a děje, které v ní probíhají, jsou lineární. Lineární závislosti jsou obvykle tím nejhrubším popisem a jsou vlastně kompromisem mezi omezenými výpočetními možnostmi a požadavky na přesné vystižení skutečnosti. V některých případech je však nepřesnost příliš velká a pak volíme přesnější model i za cenu určitých výpočetních potíží.
Za lineárními obvykle následují kvadratické modely s kvadratickou cílovou funkcí a lineárními omezujícími podmínkami. Příkladem takového modelu byl model o obsazení míst nábytkem v kuchyni. Jsou však i jiné modely, např. dopravní problém při nekonstantních sazbách. Jedná se o obvyklou situaci, kdy náklady na přepravu jednotky se mění v závislosti na množství - vezu - li 1000 cihel na nákladním autě, není to 1000x dražší, než když vezu jednu cihlu na tom samém autě. To znamená, že v některých případech je linearita absurdní.
4.4.1. Regularita,funkce Lagrangea,existence optimálního řešení.
Sestavme nyní matematický model obecné úlohy nelineárního programování.
m i n f(x)
x ![]() X
= {x
X
= {x ![]() Rn : g
(x) >= b }, kde g = ( g1 , g2
,..., gm)
Rn : g
(x) >= b }, kde g = ( g1 , g2
,..., gm)
je vektorová funkce.
Podobně jako v lineárním programování bychom mohli rozlišovat kanonický a standardní tvar úlohy. Převody typů jsou zcela analogické a my se jimi nebudeme zabývat. Podstatně důležitější je to, že požadujeme, aby cílová funkce byla konvexní a jednotlivé funkce gi byly konkávní. Tyto požadavky zaručují konvexnost množiny X a to, že lokální extrém je současně globální. Díky tomu všechny dále uvedené metody konvergují k optimálnímu řešení z libovolného nebo libovolného přípustného bodu. Nutnou pro existenci optimálního řešení je ještě i následující podmínka:
Definice 4.4.1.1
Množina X je
regulární, pokud existuje takový bod x+![]() X , že platí
X , že platí
gi(x+) > bi pro každé "i"
Definice 4.4.1.2
Funkci
L ( x, y ) = f( x ) + ( y , h ( x ) )
nazýváme funkcí Lagrangea, h ( x ) = b - g ( x ).
Definice 4.4.1.3
Bod (x*,y*) se nazývá sedlovým bodem funkce Lagrangea na množině Rn,y>=0, jestliže platí
L ( x*,y) <= L ( x*,y* ) <= L ( x , y* )
pro všechna x,y>=0.
Věta 4.4.1.1
Jestliže bod ( x*,y* ) je sedlovým bodem funkce Lagrangea, pak x* je optimálním plánem základní úlohy nelineárního programování.
Důkaz
Dosadíme do definice sedlového bodu a získáme
f(x*) + (y,h(x*)) <= f(x*) + (y*,h(x*)) <= f(x) + (y*,h(x))
Jelikož nerovnice platí pro libovolná y >= 0, tedy i pro y = 0, po úpravě získáme
f(x*) <= f(x*) + (y*,h(x*)) <= f(x) + (y*,h(x))
Pokud bod splňuje omezující podmínky, pak zřejmě
f(x*) <= f(x),
což bylo třeba dokázat.
Věta 4.4.1.2 (Věta Kuhna - Tuckera )
Předpokládejme, že množina X vyhovuje podmínce regularity. Nezbytnou a postačující podmínkou toho, aby plán x* byl optimálním plánem úlohy konvexního programování, je, aby existoval vektor y* >= 0 , takový, že bod ( x*,y* ) je sedlovým bodem funkce Lagrangea.
4.4.2. Minimalizace funkcí jedné proměnné na segmentu.
Minimalizace funkce jedné proměnné je součástí všech dalších minimalizačních metod v prostoru i na množině. Minimalizace funkcí více proměnných se určitými metodami převádí na minimalizaci funkce jedné proměnné, a proto se i my nejprve budeme zabývat metodami minimalizace funkce jedné proměnné.
Metody je možné rozdělit do několika kategorií : interpolační, aproximační, gradientní a negradientní. Nejprve se budeme zabývat negradientními metodami (nepředpokládáme, že funkce má derivaci).
Metoda prostého výběru.
Nejjednodušší a také nejhrubší metodou je metoda přímého výběru. Metoda využívá konvexnost funkce. Nechť je zadán segment [a,b] a na něm konvexní funkce f(x). Vyberme krok "h" a vytvářejme posloupnost bodů xk = xk-1 + h , kde x0 = a. Současně s určením každého bodu posloupnosti vypočteme hodnotu f(xk) a to do té doby, dokud platí f(xk-1) > f(xk). Jakmile se najde bod xk+1 takový, že f(xk+1) > f(xk), pak výpočet přerušíme, vybereme segment [xk-1,xk] a zvolíme nový, menší krok. Můžeme si představit, že máme nový interval [a',b']. Tímto způsobem pokračujeme až tak dlouho dokud velikost intervalu neklesne pod zadanou přesnost, potřebnou k výpočtu.
Procedura se dá různě modifikovat, můžeme např. krok zpočátku zvětšovat apod.
Nevýhodou tohoto postupu je poměrně velký počet výpočtů funkčních hodnot. Pokud je funkce zadána vzorcem, není to jistě žádný problém, ale pokud je funkční hodnota výsledkem experimentu, je situace jiná. Proto vzniká potřeba vytvořit metody, které by pro výpočet minima se zadanou přesností potřebovaly co nejméně výpočtů funkčních hodnot.
Fibonaciho metoda a metoda zlatého řezu.
Budeme vybírat posloupnost do sebe vložených segmentů [a0,b0],[a1,b1],..., [am,bm],... .Budeme požadovat, aby tato posloupnost měla určité vlastnosti:
A. Pro všechna 'm' je v "m"-té iteraci přiblížením optimálního řešení x* jeden z bodů ym nebo zm a pro tyto body platí následující vztah:
ym - am-1 = bm-1 - zm
Dále musí být splněny následující vztahy:
(4.4.2.1) ym = am-1 + cm-1 * ( bm-1 - am-1 )
(4.4.2.2) zm = am-1 + ( 1 - cm-1) * ( bm-1 - am-1 )
Pro čísla ci musí platit, že jsou v rozsahu 0 až 0.5 .
B. V každém kroku výpočtu je vypočítána pouze jedna hodnota f(x).
Algoritmus metody.
KROK K. V intervalu [ak,bk] určíme body yk a zk podle vztahů 4.4.2.1 a 4.4.2.2 a vypočítáme hodnoty f(yk) a f(zk).
Jestliže f(yk) < f(zk), položíme ak+1 = ak , bk+1= zk a přiblížení řešení v této iteraci xk = yk .
Jestliže f(yk) > f(zk), pak položíme ak+1 = zk , bk+1= bk a přiblížení řešení v této iteraci xk = zk .
Zásadní otázkou zůstává výběr koeficientů ck.
Fibonaciho metoda.
Nechť je naším cílem minimalizovat délku segmentu [an,bn]. Pak platí následující věta pro výběr čísel ck.
Věta 4.4.2.1
Při zadaném kriteriu je optimální vybírat tyto čísla takto:
c0 = Fn / Fn+2 ,
c1 = 1 - c0 / ( 1 - c0),
.......................
ck = (Fk - Fk+2 * c0) / (Fk-2 - Fk * c0 ).
Čísla Fi jsou Fibonaciho čísla a platí pro ně následující rekurentní vztahy
F1 = F2 = 1 , Fi = Fi-2 + Fi-1.
Důkaz
Sestavíme následující optimalizační úlohu
n-1
bn - an = ![]() ( 1 - cj) * ( b0 -
a0 )
( 1 - cj) * ( b0 -
a0 )
j=0
n-1
m i n ![]() (
1 - cj)
(
1 - cj)
j=0
0 < cj < 0.5 , j=0,1,...,n-1
1 - c1 = c0 / ( 1 - c0)
......................
1 - cj = ( Fj+1 * c0 - Fj-1) / ( Fj-2 - Fj * c0 )
Odtud pak řešením plynou vztahy,uvedené ve větě .Vztah pro hodnotu cílové funkce udává, že
bn - an = ( b0 - a0 ) / Fn+2 .
Věta je dokázána.
Pokud je zadána požadovaná přesnost výpočtu, musíme z ní nejprve určit hodnotu "n" a to z posledního vztahu.
Metoda zlatého řezu.
Výpočty čísel v předcházející metodě jsou poněkud problematické. Je možné využít buď rekurze, což je časově pro každý krok náročné, nebo si pamatovat tabulku, ale to jsou zase nároky na paměť. Vznikla otázka, jak vylepšit předcházející metodu, přitom ji zjednodušit a současně moc neztratit z optimálnosti metody. Tak vznikla metoda zlatého řezu. Vychází z toho, že všechna ck považuje za konstanty, které získáme limitním přechodem
c = lim Fn / Fn+2 = ( 3 - V 5 ) / 2 = 0.38196601125
Při dostatečně velkých "n" začínají obě metody prakticky ve stejných bodech. Pro zajímavost uvedeme hodnoty podílů pro některá n:
| n | podíl |
| 1 | 0,50 |
| 2 | 0.33333333333 |
| 3 | 0.4 |
| 4 | 0.38461538462 |
| 5 | 0.38095238095 |
| 9 | 0.38202247191 |
Uvedeme si nyní velmi efektivní gradientní metodu. Předpokládejme, že funkce má derivaci na segmentu a tato derivace je známa.
Metoda tečen.
Budeme postupovat tak, že vždy v krajních bodech segmentu určíme derivaci a funkci nahradíme tečnou v těchto bodech. Přiblížení minima bude pak průsečík těchto přímek. Odvodíme iterační vzorce:
f(x) - funkční hodnota v bodě x
f'(x)- derivace v bodě x
Rovnice přímky v bodě (x1,f(x1)):
y = k * x + q k = f'(x1)
f(x1) = f'(x1)*x1 + q = > q = f(x1) - f'(x1)*x1
y = f'(x1)*( x - x1) + f(x1)
Rovnice přímky v bodě (x2,f(x2)):
y = k * x + q k = f'(x2)
f(x2) = f'(x2)*x2 + q = > q = f(x2) - f'(x2)*x2
y = f'(x2)*( x - x2) + f(x2)
Srovnáním těchto vztahů a vyřešením rovnice získáme
x = [(f'(x1)*x1 - f'(x2)*x2) + ( f(x2) - f(x1))] / ( f'(x1)-f'(x2))
Pokud je f'(x) = 0, je x minimem. Jestliže je f'(x) < 0 , vybereme pro další řešení segment [ x , b ] ,je li f'(x) > 0, pak segment [ a , x ] a vezmeme jej za výchozí. Tímto způsobem můžeme postupovat do té doby, dokud není v bodě x dosaženo požadované přesnosti.
Interpolační metody.
Tyto metody využívají proložení interpolačního polynomu určitého stupně nalezenou skupinou bodů (podle metody, ale minimálně třemi body) a minimum tohoto polynomu považují za minimum naší funkce. Minimum musí ležet uvnitř skupiny bodů. Analogicky fungují extrapolační metody.
Následující minimalizační metody jsou sestaveny obvykle takovým způsobem, že nejprve vybereme směr minimalizace a pak aplikujeme některou z jednorozměrných minimalizačních metod na segmentu. Tím dostaneme nový bod, ve kterém opět určíme směr minimalizace a tak pokračujeme do dosažení požadované přesnosti. Jednotlivé metody se pak liší výběrem směru a použitou metodou jednorozměrné minimalizace. Obecný algoritmus vypadá následovně:
KROK 1. V bodě xk vybereme směr minimalizace (-sk).
KROK 2. (K+1) přiblížení vypočítáme podle obecného vzorce
xk+1 = xk - ßk * sk
Parametr ßk vybereme jako libovolné číslo, pro které platí
f( xk - ßk * sk ) < ( 1 - ak) * f(xk) + ak * dk,
kde a je číslo z intervalu (0,1) a
dk = m i n f( xk - ß * sk)
Pokud vezmeme hodnotu a rovnu jedné, pak je úloha převedena na minimalizaci funkce jedné proměnné.
Metoda Hookea - Jevese.
Nejjednodušší metodou výběru směru je výběr souřadnicových os. Provádíme tedy nejprve minimalizaci cílové funkce z výchozího bodu ve směru osy X, pak osy Y atd. Až projdeme všechny proměnné, vrátíme se opět k první a celý postup opakujeme. Napsat program pro takový algoritmus je elementární. Pokud má však funkce charakter úžlabiny, která nemá směr žádné souřadnicové osy, je tato metoda velmi neefektivní, a proto byla poněkud vylepšena. Funkci zobrazuje následující graf:
Metoda Rosenbrucka.
Tato metoda funguje skoro přesně tak, jako metoda předchozí. Rozdíl je v tom, že po prvních krocích se provede pootočení souřadnicových os a minimalizace probíhá pak ve směru těchto nových os. Stejně jako předchozí metoda nevyžaduje diferencovatelnost cílové funkce.
PROGRAM ROSENBRUCK;
USES CRT,PRINTER;
LABEL 1,KON,KON1;
TYPE VEKTOR=ARRAY[1..50] OF REAL;
VAR B,C,V:ARRAY[1..50] OF VEKTOR;A,D,E,R,W,X:VEKTOR;
N,KR,I,J,K,L:INTEGER;
EP,MAX,F,FF,S:REAL;
FUNCTION FUN(Y:VEKTOR):REAL;
BEGIN
FUN:=Y[1]*Y[1]+Y[2]*Y[2]
END;
BEGIN CLRSCR;WRITE('ZADEJ POCET PROMENNYCH:');READLN(N);
WRITE('ZADEJ PRESNOST VYPOCTU:');READLN(EP);
IF EP<=0 THEN EP:=1.0E-6;
WRITELN('ZADEJ VEKTOR POCATECNIHO PRIBLIZENI:');
FOR I:=1 TO N DO BEGIN WRITE(' X(',I:2,') = ');READLN(X[I]);END;
KR:=0;FF:=FUN(X);
FOR I:=1 TO N DO FOR J:=1 TO N DO IF I=J THEN V[I,J]:=1.0 ELSE
V[I,J]:=0.0;
1:FOR I:=1 TO N DO BEGIN A[I]:=2;D[I]:=0;E[I]:=0.1 END;
REPEAT I:=1 ;KR:=KR+1;
REPEAT FOR J:=1 TO N DO BEGIN X[J]:=X[J]+E[I]*V[I,J];W[J]:=X[J] END;
F:=FUN(X);IF F<FF THEN BEGIN D[I]:=D[I]+E[I]*(1+FF-F);
E[I]:=3*E[I];FF:=F;IF A[I]>1.5 THEN A[I]:=1 END
ELSE BEGIN FOR J:=1 TO N DO X[J]:=X[J]-E[I]*V[I,J];
E[I]:=-0.5*E[I];IF A[I]<1.5 THEN A[I]:=0 END;
MAX:=0.0;FOR J:=1 TO N DO IF MAX<ABS(E[J]) THEN MAX:=ABS(E[J]);
IF MAX<EP THEN GOTO KON;
FOR K:=1 TO N DO IF A[K]>0.5 THEN GOTO KON1;
FOR L:=1 TO N DO FOR J:=1 TO N DO BEGIN S:=0;
FOR K:=L TO N DO S:=S+D[K]*V[K,J];C[L,J]:=S END;
FOR L:=1 TO N DO BEGIN IF L<>1 THEN BEGIN
FOR J:=1 TO L-1 DO BEGIN S:=0;FOR K:=1 TO N DO
S:=S+C[L,K]*V[J,K];R[J]:=S END END;
FOR J:=1 TO N DO BEGIN B[L,J]:=C[L,J];IF L<>1 THEN
FOR K:=1 TO L-1 DO
B[L,J]:=B[L,J]-R[K]*V[K,J] END;
S:=0;FOR J:=1 TO N DO S:=S+B[L,J]*B[L,J];
S:=SQRT(S);
IF S<0.00001 THEN S:= 0.00001;FOR J:=1 TO N DO
V[L,J]:=B[L,J]/S END;
GOTO 1;
KON1:I:=I+1 UNTIL I>N;
UNTIL FALSE;
KON:WRITELN('R E S E N I :');
WRITELN('***************************************');
WRITELN('HODNOTA CILOVE FUNKCE:',FUN(X));
FOR I:=1 TO N DO WRITELN('X(',I:2,') = ',X[I]);
WRITELN('POCET ITERACI METODY:',KR:5);
WRITELN('****************************************')
end.
Výsledky výpočtu kontrolní úlohy:
R E S E N I :
***************************************
HODNOTA CILOVE FUNKCE: 4.9953245199E-10
X( 1) = 1.9945549639E-06
X( 2) = -2.2261046752E-05
POCET ITERACI METODY: 72
****************************************
Metoda Davidona - Fletchera - Powella.
Tato metoda je tzv. metodou změny metriky. Podle průběhu výpočtu se změní metrické vztahy co se týče os i měřítka. Program patří k nejefektivnějším metodám, které nevyužívají gradient.
PROGRAM DAVIDON_FLETCHER_POWELL;
USES CRT,PRINTER;
LABEL 1,2,KON;
TYPE VEKTOR=ARRAY[1..50] OF REAL;
VAR G:ARRAY[1..50] OF VEKTOR;DE,GR,GJ,S,W,X,X1,X2,Y,Z:VEKTOR;
N,KR,I,J,K,L:INTEGER;
EP,EO,DEL,F,E1,E2,A,A1,A2,GN,D1,D2 :REAL;
FUNCTION FUN(Y:VEKTOR):REAL;
BEGIN
FUN:=Y[1]*Y[1]+Y[2]*Y[2]
END;
BEGIN CLRSCR;WRITE('ZADEJ POCET PROMENNYCH:');READLN(N);
WRITE('ZADEJ PRESNOST VYPOCTU:');READLN(EP);
IF EP<=0 THEN EP:=1.0E-6;
WRITELN('ZADEJ VEKTOR POCATECNIHO PRIBLIZENI:');
FOR I:=1 TO N DO BEGIN WRITE(' X(',I:2,') = ');READLN(X[I]);END;
KR:=0;EO:=FUN(X);
1:FOR I:=1 TO N DO W[I]:=X[I];
FOR I:=1 TO N DO BEGIN DEL:=EP*X[I];
IF ABS(X[I])<=EP THEN DEL:=EP;
W[I]:=X[I]+DEL;F:=FUN(W);GR[I]:=(F-EO)/DEL;
W[I]:=X[I] END;K:=0;
FOR I:=1 TO N DO FOR J:=1 TO N DO IF I=J THEN G[I,J]:=1 ELSE G[I,J]:=0;
REPEAT FOR I:=1 TO N DO BEGIN S[I]:=0;
FOR J:=1 TO N DO S[I]:=S[I]-G[I,J]*GR[J] END;A1:=1.0;
WHILE A1>EP*EP DO BEGIN FOR I:=1 TO N DO BEGIN
X1[I]:=X[I]+A1*S[I];W[I]:=X1[I] END;
F:=FUN(W);E1:=F;IF E1<=EO THEN GOTO 2;A1:=A1/2.0 END;
2:A2:=A1;E2:=E1;WHILE E2<=E1 DO BEGIN
A2:=A1*2.0;FOR I:=1 TO N DO BEGIN X2[I]:=X[I]+A2*S[I];
W[I]:=X2[I] END;F:=FUN(W);E2:=F;
IF E2<=E1 THEN BEGIN A1:=A2;E1:=E2 END END;
IF A1=A2 THEN A1:=A2+EP;
A:=(A1*A1-A2*A2)*EO+A2*A2*E1-A1*A1*E2;
A:=A/((A1-A2)*EO+A2*E1-A1*E2)/2.0;
FOR I:=1 TO N DO BEGIN DE[I]:=A*S[I];X[I]:=X[I]+DE[I];W[I]:=X[I]
END;
F:=FUN(W);EO:=F;
IF EO>=E1 THEN BEGIN FOR I:=1 TO N DO BEGIN
X[I]:=X[I]+(A1-A)*S[I];W[I]:=X[I];DE[I]:=A1*S[I] END;
F:=FUN(W);EO:=F END;
KR:=KR+1;K:=K+1;IF K=5 THEN GOTO 1;
FOR I:=1 TO N DO W[I]:=X[I];
FOR I:=1 TO N DO BEGIN DEL:=X[I]*EP;IF ABS(X[I])<EP THEN DEL:=EP;
W[I]:=X[I]+DEL;F:=FUN(W);GJ[I]:=(F-EO)/DEL;
W[I]:=X[I] END;
GN:=0;FOR I:=1 TO N DO GN:=GN+GJ[I]*GJ[I];
IF GN<=EP THEN GOTO KON;
FOR I:=1 TO N DO BEGIN Y[I]:=GJ[I]-GR[I];GR[I]:=GJ[I] END;
D1:=0;FOR I:=1 TO N DO D1:=D1+Y[I]*DE[I];
FOR I:=1 TO N DO BEGIN Z[I]:=0;FOR J:=1 TO N DO
Z[I]:=Z[I]+G[I,J]*Y[J] END;D2:=0;
FOR I:=1 TO N DO FOR J:=1 TO N DO D2:=D2+G[I,J]*Y[I]*Y[J];
FOR I:=1 TO N DO FOR J:=1 TO N DO
G[I,J]:=G[I,J]+DE[I]*DE[J]/(D1+EP)-Z[I]*Z[J]/(D2+EP)
UNTIL FALSE;
KON:WRITELN('R E S E N I :');
WRITELN('***************************************');
WRITELN('HODNOTA CILOVE FUNKCE:',FUN(X));
FOR I:=1 TO N DO WRITELN('X(',I:2,') = ',X[I]);
WRITELN('POCET ITERACI METODY:',KR:5);
WRITELN('****************************************')
END.
Výsledky
výpočtu kontrolní úlohy:
R E S E N I :
***************************************
HODNOTA CILOVE FUNKCE: 3.9837956654E-16
X( 1) = 1.0266376194E-08
X( 2) = -1.7116690287E-08
POCET ITERACI METODY: 1
****************************************
Metoda DFP v JavaScriptu s interaktivním zadáním funkce...Z dalších používaných metod převažují gradientní metody a to metoda největšího spádu a metoda konjugovaných gradientů. Metoda největšího spádu vybírá jako směr minimalizace směr antigradientu cílové funkce - grad ( f(x) ). Pokud je funkce úžlabinového tvaru a výpočet minimalizace ve směru není absolutně přesný, má metoda velmi mnoho iterací a výpočet je neefektivní. Z těchto důvodů uvedu pouze druhou metodu.
Metoda konjugovaných (sdružených) gradientů.
Zvláštností metody je, že při přesné jednorozměrné minimalizaci řeší kvadratické cílové funkce za počet kroků menší nebo roven rozměru prostoru. Směr minimalizace se určuje podle následujících vzorců:
s0 = grad ( f ( x0 )) , sk = grad ( f ( xk)) + dk * sk-1
Metoda si tedy pamatuje určitou historii a využívá i předcházející směry minimalizace. Metoda není konečná pro libovolné parametry. Konečnost řešení minimalizace kvadratické funkce je zaručena např. při:
||grad ( f (xk))|| ^2
dk = ----------------------------------------
||grad ( f (xk-1)) ||^2
Metodu realizuje následující program
PROGRAM KONJU;
TYPE VEK=ARRAY[1..50] OF REAL;
VAR N,I,L:INTEGER;
F,S,E,DEL,GE:REAL;
X,XP,G,G1:VEK;
FUNCTION SKAL(V:VEK):REAL;
VAR I:INTEGER;S:REAL;
BEGIN S:=0;FOR I:=1 TO N DO
S:=S+V[I]*V[I];SKAL:=S END;
FUNCTION FUN(Y:VEK):REAL;
VAR I:INTEGER;S:REAL;
BEGIN S:=0;FOR I:=1 TO N DO
S:=S+(Y[I]-I)*(Y[I]-I)*(Y[I]-I)*(Y[I]-I);
FUN:=S END;
PROCEDURE GRAD(Y:VEK;VAR G:VEK);
VAR I:INTEGER;
BEGIN FOR I:=1 TO N DO G[I]:=
4*(Y[I]-I)*(Y[I]-I)*(Y[I]-I) END;
BEGIN READLN(N,E);FOR I:=1 TO N DO READLN(X[I]);
GRAD(X,G);S:=SKAL(G);
WHILE S>E DO BEGIN DEL:=200*E;L:=1;WHILE DEL>E DO BEGIN
FOR I:=1 TO N DO XP[I]:=X[I]-DEL*G[I];F:=FUN(XP);
IF FUN(XP)<FUN(X) THEN BEGIN
X:=XP;DEL:=2*DEL END ELSE
DEL:=DEL/1.324 END;
GRAD(X,G1);IF L=N THEN BEGIN L:=1;G:=G1 END
ELSE BEGIN GE:=SKAL(G1)/SKAL(G);FOR I:=
1 TO N DO G[I]:=G1[I]+GE*GE*G[I];L:=L+1 END;
S:=SKAL(G) END;
WRITELN('R E S E N I:');
FOR I:=1 TO N DO WRITELN('X[',I:2,']=',X[I]:12:8);
WRITELN('FUNKCNI HODNOTA:',F:12:8);
WRITELN('GRADIENT:');
FOR I:=1 TO N DO WRITELN('G(',I:2,')=',G[I])
END.
Výsledky
výpočtu kontrolní úlohy:
R E S E N I:
X[ 1]= 0.92555202
X[ 2]= 2.09489371
FUNKCNI HODNOTA: 0.00011183
GRADIENT:
G( 1)=-1.6504664055E-03
G( 2)= 3.4180028826E-03
Metody mohou být upraveny také tak, že
místo zadání gradientu ve formě
matematického vzorce je gradient
vypočítán numericky z funkčních
hodnot.
Takto upravené metody se pak obvykle
nazývají subgradientní nebo metodami
s numerickým výpočtem gradientu. Postupuje se tak
v případech, kdy nemáme
zadánu funkci vzorcem, ale
předpokládáme, že je diferencovatelná
nebo v
případech, kdy je výpočet gradientu
příliš složitý.
V předchozím odstavci jsme vpodstatě neměli potíže s určením směru minimalizace. Při omezujících podmínkách je situace jiná. Nesmíme se dostat mimo určenou oblast. Dalším problémem může být určení výchozího bodu pro optimalizační metodu. Není vždy snadné najít bod, který by vyhovoval všem omezujícím podmínkám úlohy.
Nejjednodušší způsob řešení dané situace je převedení těchto úloh na úlohy bez omezujících podmínek. Využíváme k tomu tzv. penalizující funkci.
Definice 4.4.4.1
Spojitou funkci M(ß,x) = f(x) + (1/ß) * p(x) definovanou na R1 x Rn nazveme vnější penalizující funkcí pro základní úlohu konvexního programování, jestliže platí:
1. p(x) = 0 , x ![]() X
,X je množinou
přípustných řešení
úlohy
X
,X je množinou
přípustných řešení
úlohy
1. p(x) > 0 , v ostatních případech
Uveďme si některé případy používaných penalizujících funkcí:
p(x) = ![]() m i n {gi(x)
; 0 } 2
m i n {gi(x)
; 0 } 2
i
p(x) = exp [ ![]() m
i n {gi(x) ; 0 }]
m
i n {gi(x) ; 0 }]
i
Další postup je založen na řešení posloupnosti úloh M ( ßk, x ), takových, že parametr ßk se postupně blíží k nule. To znamená, že zvolíme nějakou hodnotu parametru, vyřešíme minimalizační úlohu bez omezujících podmínek. Pak mohou nastat dvě možnosti :
1. Řešení vyhovuje omezujícím podmínkám se zadanou přesností a pak je řešení ukončeno nebo
2. Řešení nevyhovuje, snížíme tedy hodnotu parametru např. o polovinu a vezmeme nalezené optimální řešení za výchozí a minimalizujeme novou cílovou funkci M.
Tento postup opakujeme do té doby, dokud nedosáhneme požadované přesnosti řešení. Platí následující věta:
Věta 4.4.4.1
Jestliže původní úloha a posloupnost parametrických úloh mají optimální řešení, pak
l i m M( xk ,ßk ) = f ( xk ) a l i m xk = x*
Následující programy realizují předchozí metody s použitím vnější penalizující funkce. Funkci M znázorňuje následující obrázek. Je zřejmé, že kolem množiny má funkce úvalový charakter.
PROGRAM KONJU; {konjugované gradienty s omezujícími podmínkami rovnice i nerov.}
USES CRT;
LABEL KON;
CONST LIM=50;
{S OMEZUJICIMI PODMINKAMI}
TYPE VEK=ARRAY[1..50] OF REAL;
VAR KR,N,I,L,MM,NN,L1:INTEGER;
F,S,E,DEL,GE,AP,EP,CC:REAL;
XX,X,XP,G,G1:VEK;
H:TEXT;
FUNCTION SKAL(V:VEK):REAL;
VAR I:INTEGER;S:REAL;
BEGIN S:=0;FOR I:=1 TO N DO
S:=S+V[I]*V[I];SKAL:=S END;
FUNCTION FFF(Y:VEK;I:INTEGER):REAL;{zadani funkce a omezujicich podminek}
BEGIN CASE I OF 0:FFF:=Y[1]*Y[1]*Y[1]*Y[1]+Y[2]*Y[2];
1:FFF:=Y[1]-2;
2:FFF:=Y[2]+3;
3:FFF:=Y[1]-2*Y[2]-5;
END
END;
PROCEDURE GM(Y:VEK;I:INTEGER;VAR GR:VEK);{zde jsou zadany gradienty}
BEGIN CASE I OF 0:BEGIN GR[1]:=-4*Y[1]*Y[1]*Y[1];GR[2]:=-2*Y[2] END;
1:BEGIN GR[1]:=-1;GR[2]:=0 END;
2:BEGIN GR[1]:=0;GR[2]:=-1 END;
3:BEGIN GR[1]:=-1;GR[2]:=2 END;
END;
END;
FUNCTION FUN(Y:VEK):REAL;
VAR S,S1:REAL;
BEGIN S1:=0;FOR I:=1 TO MM+NN DO BEGIN
S:=FFF(Y,I);IF (I<=MM) AND (S<0) THEN S1:=S1+S*S;
IF I>MM THEN S1:=S1+S*S END;
FUN:=FFF(Y,0)+CC*S1
END;
PROCEDURE GRAD(Y:VEK;VAR G:VEK);
VAR I,J:INTEGER;GR:VEK;S,S1:REAL;
BEGIN S1:=0;FOR J:=1 TO N DO BEGIN FOR I:=1 TO MM+NN DO BEGIN
S:=FFF(Y,I);GM(Y,I,GR);IF (I<=MM) AND (S<0) THEN S1:=S1+GR[J]*2*S;
IF (I>MM) AND (S<>0) THEN S1:=S1+2*GR[J]*S END;
GM(Y,0,GR);G[J]:=GR[J]+CC*S1 END;
END;
PROCEDURE KVADR(D:VEK;VAR X:VEK);
CONST LIMIT=3;
VAR TAU,TAUA,T0,T,G0,G:REAL;L,I:INTEGER;B:BOOLEAN;
XP:VEK;
FUNCTION GRD(X,D:VEK;TAU:REAL):REAL;
VAR XA,XB:VEK;I:INTEGER;
BEGIN FOR I:=1 TO N DO BEGIN XA[I]:=X[I]+(TAU+E/100)*D[I];
XB[I]:=X[I]+TAU*D[I] END;
GRD:=(FUN(XA)-FUN(XB))/(E/100)
END;
{alternativni cast procedury}
{BEGIN T0:=E;TAUA:=0;L:=1;
WHILE (ABS(GRD(X,D,TAUA))>E) AND (L<=LIMIT) DO BEGIN
G0:=GRD(X,D,TAUA);L:=L+1;B:=TRUE;
IF GRD(X,D,TAUA)>0 THEN BEGIN TAU:=-T0+TAUA;
WHILE GRD(X,D,TAU)>0 DO BEGIN G0:=GRD(X,D,TAU);
B:=FALSE;TAUA:=TAU;TAU:=2*TAU END END
ELSE BEGIN TAU:=T0+TAUA;
WHILE GRD(X,D,TAU)<0 DO BEGIN G0:=GRD(X,D,TAU);TAUA:=TAU;
B:=FALSE;TAU:=2*TAU END END;T:=TAUA;
G:=GRD(X,D,TAU);TAUA:=TAUA-G0*(TAUA-TAU)/(G0-G);
WRITELN(TAU,TAUA,G,G0);IF B AND (T0>ABS(T-TAUA))THEN T0:=T0/5 END;
FOR I:=1 TO N DO X[I]:=X[I]+TAUA*D[I]
END;}
{realne pracujici cast procedury}
BEGIN DEL:=200*EP;T0:=DEL;TAUA:=SQRT(SKAL(D));
IF GRD(X,D,0)>0 THEN TAU:=-T0 ELSE TAU:=T0;G0:=FUN(X);
WHILE ABS(TAU)>EP/100 DO BEGIN
FOR I:=1 TO N DO XP[I]:=X[I]+TAU*D[I]/TAUA;G:=FUN(XP);
IF G0>G THEN BEGIN X:=XP;G0:=G;TAU:=2.7132*TAU END
ELSE TAU:=TAU/3.0 END
END;
{ Hlavni program}
BEGIN CLRSCR;WRITE('ZADEJ POCET PROMENNYCH:');READLN(N);
WRITELN('OMEZUJICI PODMINKY:');ASSIGN(H,'KONJUOM.TXT');REWRITE(H);
WRITE('ZADEJ POCET NEROVNIC >=0:');READLN(MM);
WRITE('ZADEJ POCET ROVNIC =0:');READLN(NN);
WRITE('ZADEJ PRESNOST VYPOCTU:');READLN(AP);
IF AP<=0 THEN AP:=1.0E-9;E:=AP;
WRITELN('ZADEJ VEKTOR POCATECNIHO PRIBLIZENI:');
FOR I:=1 TO N DO BEGIN WRITE(' X(',I:2,') = ');READLN(X[I]);END;
KR:=0;EP:=3*AP;CC:=5;
REPEAT CC:=CC*2;IF AP<EP THEN EP:=EP/2;XX:=X;
GRAD(X,G);S:=SKAL(G);L:=1;L1:=1;
WHILE SQRT(S)>EP DO BEGIN KVADR(G,X);KR:=KR+1;L1:=L1+1;IF L1>LIM/2 THEN
GOTO KON;
GRAD(X,G1);IF L=N THEN BEGIN L:=1;G:=G1 END
ELSE BEGIN GE:=SKAL(G1)/SKAL(G);FOR I:=
1 TO N DO IF GE<1.0E10 THEN G[I]:=G1[I]+GE*G[I];L:=L+1 END;
S:=SKAL(G) END;
KON:WRITELN(H,'ITERACE:',KR:5);L1:=1;
FOR I:=1 TO N DO WRITELN(H,'X[',I:2,']=',X[I]:12:8);
WRITELN(H,'FUNKCNI HODNOTA PEN.F-CE:',FUN(X):12:8);
WRITELN(H,'FUNKCNI HODNOTA CIL.F-CE:',FFF(X,0));
WRITELN(H,'OMEZUJICI PODMINKY: NEROVNICE');FOR I:=1 TO MM DO
WRITELN(H,'NEROVNICE ',I:2,' HODNOTA:',FFF(X,I));
WRITELN(H,'OMEZUJICI PODMINKY: ROVNICE');FOR I:=MM+1 TO MM+NN DO
WRITELN(H,'ROVNICE ',I-MM:2,' HODNOTA ',FFF(X,I));
WRITELN(H,'GRADIENT:');
FOR I:=1 TO N DO WRITELN(H,'G(',I:2,')=',G[I]);
WRITELN(H,S);
WRITELN(FFF(XX,0),FFF(X,0));
UNTIL (SQRT(S)<AP) OR (limit*10<kr) OR (ABS(FFF(XX,0)-FFF(X,0))<AP/100.0);
WRITELN(H,'R E S E N I :');
WRITELN(H,'***************************************');
WRITELN(H,'HODNOTA CILOVE FUNKCE:',FFF(X,0));
FOR I:=1 TO N DO WRITELN(H,'X(',I:2,') = ',X[I]);
WRITELN(H,'POCET ITERACI METODY:',KR:5);
WRITELN(H,'OMEZUJICI PODMINKY: NEROVNICE');FOR I:=1 TO MM DO WRITELN(H,'NEROVNICE ',I:2,' HODNOTA:',FFF(X,I));
WRITELN(H,'OMEZUJICI PODMINKY: ROVNICE');FOR I:=MM+1 TO MM+NN DO
WRITELN(H,'ROVNICE ',I-MM:2,' HODNOTA ',FFF(X,I));
WRITELN(H,'****************************************')
;CLOSE(H)
END.
Omezující podmínky mohou být zadávány jako rovnice i jako nerovnice.
Výsledky výpočtu kontrolní úlohy:
Zadané údaje: počet proměnných 2
počet nerovnic 2
počet rovnic 1
požadovaná přesnost 0.01
ITERACE: 25
X[ 1]= 1.65837335
X[ 2]= -1.43421401
FUNKCNI HODNOTA PEN.F-CE: 13.02683890
FUNKCNI HODNOTA CIL.F-CE: 9.6205817554E+00
OMEZUJICI PODMINKY: NEROVNICE
NEROVNICE 1 HODNOTA:-3.4162665198E-01
NEROVNICE 2 HODNOTA: 1.5657859899E+00
OMEZUJICI PODMINKY: ROVNICE
ROVNICE 1 HODNOTA -4.7319863184E-01
GRADIENT:
G( 1)=-1.9587229368E+00
G( 2)= 2.3775980309E-01
3.8931252671E+00
ITERACE: 50
X[ 1]= 1.69091804
X[ 2]= -1.48523141
FUNKCNI HODNOTA PEN.F-CE: 14.58485033
FUNKCNI HODNOTA CIL.F-CE: 1.0380958849E+01
OMEZUJICI PODMINKY: NEROVNICE
NEROVNICE 1 HODNOTA:-3.0908195864E-01
NEROVNICE 2 HODNOTA: 1.5147685869E+00
OMEZUJICI PODMINKY: ROVNICE
ROVNICE 1 HODNOTA -3.3861913253E-01
GRADIENT:
G( 1)= 6.5693263368E+00
G( 2)= 1.7889758704E+00
4.6356483185E+01
ITERACE: 75
X[ 1]= 1.78840897
X[ 2]= -1.59352988
FUNKCNI HODNOTA PEN.F-CE: 14.58404441
FUNKCNI HODNOTA CIL.F-CE: 1.2769142441E+01
OMEZUJICI PODMINKY: NEROVNICE
NEROVNICE 1 HODNOTA:-2.1159103429E-01
NEROVNICE 2 HODNOTA: 1.4064701198E+00
OMEZUJICI PODMINKY: ROVNICE
ROVNICE 1 HODNOTA -2.4531273899E-02
GRADIENT:
G( 1)=-3.9904517075E+00
G( 2)= 1.8151840592E+01
3.4541302169E+02
ITERACE: 100
X[ 1]= 1.79094164
X[ 2]= -1.58790053
FUNKCNI HODNOTA PEN.F-CE: 16.39422015
FUNKCNI HODNOTA CIL.F-CE: 1.2809304382E+01
OMEZUJICI PODMINKY: NEROVNICE
NEROVNICE 1 HODNOTA:-2.0905836382E-01
NEROVNICE 2 HODNOTA: 1.4120994650E+00
OMEZUJICI PODMINKY: ROVNICE
ROVNICE 1 HODNOTA -3.3257293915E-02
GRADIENT:
G( 1)= 1.5792925031E+01
G( 2)= 3.1303972255E+01
1.2293551600E+03
ITERACE: 125
X[ 1]= 1.94639721
X[ 2]= -1.49725312
FUNKCNI HODNOTA PEN.F-CE: 17.61271788
FUNKCNI HODNOTA CIL.F-CE: 1.6594212013E+01
OMEZUJICI PODMINKY: NEROVNICE
NEROVNICE 1 HODNOTA:-5.3602788661E-02
NEROVNICE 2 HODNOTA: 1.5027468828E+00
OMEZUJICI PODMINKY: ROVNICE
ROVNICE 1 HODNOTA -5.9096554323E-02
GRADIENT:
G( 1)= 6.5683814546E+00
G( 2)= 1.2365012224E+00
4.4672570206E+01
ITERACE: 150
X[ 1]= 1.95595405
X[ 2]= -1.52084055
FUNKCNI HODNOTA PEN.F-CE: 17.57197106
FUNKCNI HODNOTA CIL.F-CE: 1.6949366957E+01
OMEZUJICI PODMINKY: NEROVNICE
NEROVNICE 1 HODNOTA:-4.4045945950E-02
NEROVNICE 2 HODNOTA: 1.4791594480E+00
OMEZUJICI PODMINKY: ROVNICE
ROVNICE 1 HODNOTA -2.3648419447E-03
GRADIENT:
G( 1)=-2.2910962606E-01
G( 2)= 2.9717587667E+01
8.8318750798E+02
ITERACE: 175
X[ 1]= 1.98754118
X[ 2]= -1.49894362
FUNKCNI HODNOTA PEN.F-CE: 18.08709379
FUNKCNI HODNOTA CIL.F-CE: 1.7851859580E+01
OMEZUJICI PODMINKY: NEROVNICE
NEROVNICE 1 HODNOTA:-1.2458820913E-02
NEROVNICE 2 HODNOTA: 1.5010563844E+00
OMEZUJICI PODMINKY: ROVNICE
ROVNICE 1 HODNOTA -1.4571589731E-02
GRADIENT:
G( 1)= 3.1932314297E+00
G( 2)= 2.9354314437E-01
1.0282894541E+01
R E S E N I :
***************************************
HODNOTA CILOVE FUNKCE: 1.7851859580E+01
X( 1) = 1.9875411791E+00
X( 2) = -1.4989436156E+00
POCET ITERACI METODY: 175
OMEZUJICI PODMINKY: NEROVNICE
NEROVNICE 1 HODNOTA:-1.2458820913E-02
NEROVNICE 2 HODNOTA: 1.5010563844E+00
OMEZUJICI PODMINKY: ROVNICE
ROVNICE 1 HODNOTA -1.4571589731E-02
****************************************
Analogické úpravy je možné provést i v metodách Rosenbrucka a DFP, ale je třeba dát pozor na vazby jednotlivých parametrů metody.
4.5. Nekonvexní programování.Mnohoextremální úlohy.
I když se většina prací nelineárního programování zabývá především konvexními úlohami, existují i úlohy s nekonvexní cílovou funkcí a úlohy na nekonvexních množinách. Řešení těchto problémů je obtížné a zdlouhavé. Vyžaduje dostatečnou operační paměť počítače a dostatečný čas pro řešení. Existují různé metody, jak tyto problémy řešit. Lze použít lokální metody z různých výchozích bodů nebo globální metody, které jsou založeny na zhušťování nerovnoměrné sítě. Jsou to především informačně-stochastické metody.
Příkladem takového programu pro funkci dvou proměnných, který využívá tvorby nerovnoměrné trojúhelníkové sítě, je následující program s grafickým výstupem. Přibližně získaný bod je možné upřesnit lokální metodou.
PROGRAM GLOBA2;
USES CRT,DOS,GRAPH3,GRAPH;
CONST BODY=1000;
TYPE TROJ=RECORD X,Y,Z:ARRAY[1..3] OF REAL;P:REAL END;
VAR SIT:ARRAY[1..BODY] OF TROJ;
XX,YY,ZZ:TROJ;
II,NN,M,N,I,J,JJ,IJ:INTEGER;
MINMINOR,EPS,PLOCHA,FMIN,XMIN,YMIN:REAL;
Q,P,L:BOOLEAN;
FUNCTION F(CX,CY:REAL):REAL;
BEGIN F:=CX*CX+CY*CY;JJ:=JJ+1
;M:=20 END;
PROCEDURE DRAWTROJ(I:INTEGER);
VAR IX1,IX2,IY1,IY2,IX3,IY3:INTEGER;
BEGIN WITH SIT[I] DO BEGIN IX1:=ROUND((X[1]+5)/10*639);
IY1:=ROUND(199-(Y[1]+5)/10*199);
IX2:=ROUND((X[2]+5)/10*639);
IY2:=ROUND(199-(Y[2]+5)/10*199);
IX3:=ROUND((X[3]+5)/10*639);
IY3:=ROUND(199-(Y[3]+5)/10*199);
END;
DRAW(IX1,IY1,IX2,IY2,1);DRAW(IX1,IY1,IX3,IY3,1);DRAW(IX2,IY2,IX3,IY3,1);
END;
PROCEDURE AREA(I:INTEGER);
VAR A,B,C,P1,ALPA,PL:REAL;
BEGIN WITH SIT[I] DO BEGIN
A:=SQRT(SQR(X[2]-X[3])+SQR(Y[2]-Y[3]));
B:=SQRT(SQR(X[1]-X[3])+SQR(Y[1]-Y[3]));
C:=SQRT(SQR(X[2]-X[1])+SQR(Y[2]-Y[1])) END;
{ P1:=(SQR(B)+SQR(C)-SQR(A))/(2*B*C);
ALPA:=ABS(ARCTAN(SQRT(1-SQR(P1))/P1));
PL:=B*C*SIN(ALPA)/2;} PL:=A+B+C;
IF PLOCHA>PL THEN PLOCHA:=PL
END;
FUNCTION MINOR(I:INTEGER):REAL;
TYPE VEK=ARRAY[1..2] OF REAL;
VAR J:INTEGER;XY,YZ,XZ,PP,XP,S:VEK;LP:BOOLEAN;T,F1,F,E,DEL:REAL;
PROCEDURE FUN(O:VEK;VAR F:REAL);
VAR DET,ALPA,BETA:REAL;
BEGIN WITH SIT[I] DO BEGIN DET:=(X[1]-X[3])*(Y[2]-Y[3])-(Y[1]-Y[3])*(X[2]-X[3]);
ALPA:=((O[1]-X[3])*(Y[2]-Y[3])-(O[2]-Y[3])*(X[2]-X[3]))
/DET;
BETA:=((X[1]-X[3])*(O[2]-Y[3])-(Y[1]-Y[3])*(O[1]-X[3]))
/DET;
END;
IF (ALPA>=0) AND (BETA>=0) AND (ALPA+BETA<=1) THEN
BEGIN F:=SIT[I].Z[1]-M*SQRT(SQR(SIT[I].X[1]-O[1])
+SQR(SIT[I].Y[1]-O[2]));
IF F<SIT[I].Z[2]-M*SQRT(SQR(SIT[I].X[2]-O[1])
+SQR(SIT[I].Y[2]-O[2])) THEN
F:=SIT[I].Z[2]-M*SQRT(SQR(SIT[I].X[2]-O[1])
+SQR(SIT[I].Y[2]-O[2]));
IF F<SIT[I].Z[3]-M*SQRT(SQR(SIT[I].X[3]-O[1])
+SQR(SIT[I].Y[3]-O[2])) THEN
F:=SIT[I].Z[3]-M*SQRT(SQR(SIT[I].X[3]-O[1])
+SQR(SIT[I].Y[3]-O[2]));
END
ELSE F:=1.0E5
END;
BEGIN WITH SIT[I] DO BEGIN
XY[1]:=(X[1]+X[2])/2+(Z[1]-Z[2])/(2*M);
XY[2]:=(Y[1]+Y[2])/2+(Z[1]-Z[2])/(2*M);
XZ[1]:=(X[1]+X[3])/2+(Z[1]-Z[3])/(2*M);
XZ[2]:=(Y[1]+Y[3])/2+(Z[1]-Z[3])/(2*M);
YZ[1]:=(X[2]+X[3])/2+(Z[2]-Z[3])/(2*M);
YZ[2]:=(Y[2]+Y[3])/2+(Z[2]-Z[3])/(2*M);
T:=(XZ[1]*(X[3]-X[1])-XZ[2]*(Y[1]-Y[3])+XY[2]*(Y[1]-Y[3])-XY[1]*(X[3]-X[1]))/
((Y[1]-Y[2])*(X[3]-X[1])+(X[1]-X[2])*(Y[1]-Y[3]));
PP[1]:=XY[1]+T*(Y[1]-Y[2]);PP[2]:=XY[2]+T*(X[2]-X[1]);
END;
{X[1]:=(SIT[I].X[1]+SIT[I].X[2]+SIT[I].X[3])/3;
X[2]:=(SIT[I].Y[1]+SIT[I].Y[2]+SIT[I].Y[3])/3;S:=X;
DEL:=0.1;LP:=TRUE;
WHILE LP OR (DEL>0.0003) DO BEGIN
LP:=FALSE;FOR J:=1 TO 2 DO BEGIN
FUN(X,F);XP:=X;XP[J]:=X[J]+DEL;FUN(XP,F1);
IF F1<F THEN BEGIN X:=XP;LP:=TRUE END;
XP:=X;FUN(X,F);
XP[J]:=X[J]-DEL;FUN(XP,F1);
IF F1<F THEN BEGIN X:=XP;LP:=TRUE END END;
IF NOT LP THEN DEL:=DEL/2 END;FUN(X,F);}FUN(PP,F);
MINOR:=F;IF F>=1.0E4 THEN BEGIN FUN(XY,F1);IF F1<F THEN F:=F1;
FUN(XZ,F1);IF F1<F THEN F:=F1;FUN(YZ,F1);IF F1<F THEN F:=F1;
MINOR:=F END
END;
PROCEDURE ROZDEL;
VAR XX,YY,ZZ:TROJ;
BEGIN IJ:=IJ+3;WITH SIT[N] DO BEGIN
XX.X[1]:=X[1];XX.Y[1]:=Y[1];XX.Z[1]:=Z[1];
XX.X[2]:=(X[1]+X[2])/2+(Z[1]-Z[2])/(2*M);;
XX.Y[2]:=(Y[1]+Y[2])/2+(Z[1]-Z[2])/(2*M);;XX.Z[2]:=F(XX.X[2],XX.Y[2]);
XX.X[3]:=(X[1]+X[3])/2+(Z[1]-Z[3])/(2*M);
;XX.Y[3]:=(Y[1]+Y[3])/2+(Z[1]-Z[3])/(2*M);;XX.Z[3]:=F(XX.X[3],XX.Y[3]);
YY.X[1]:=(X[1]+X[2])/2+(Z[1]-Z[2])/(2*M);
;YY.Y[1]:=(Y[1]+Y[2])/2+(Z[1]-Z[2])/(2*M);;YY.Z[1]:=F(YY.X[1],YY.Y[1]);
YY.X[2]:=X[2];YY.Y[2]:=Y[2];YY.Z[2]:=Z[2];
YY.X[3]:=(X[2]+X[3])/2+(Z[2]-Z[3])/(2*M);
;YY.Y[3]:=(Y[2]+Y[3])/2+(Z[2]-Z[3])/(2*M);;YY.Z[3]:=F(YY.X[3],YY.Y[3]);
ZZ.X[1]:=(X[1]+X[3])/2+(Z[1]-Z[3])/(2*M);
;ZZ.Y[1]:=(Y[1]+Y[3])/2+(Z[1]-Z[3])/(2*M);;ZZ.Z[1]:=F(ZZ.X[1],ZZ.Y[1]);
ZZ.X[2]:=(X[2]+X[3])/2+(Z[2]-Z[3])/(2*M);
;ZZ.Y[2]:=(Y[2]+Y[3])/2+(Z[2]-Z[3])/(2*M);;ZZ.Z[2]:=F(ZZ.X[2],ZZ.Y[2]);
ZZ.X[3]:=X[3];ZZ.Y[3]:=Y[3];ZZ.Z[3]:=F(ZZ.X[3],ZZ.Y[3]);
X[1]:=XX.X[2];Y[1]:=XX.Y[2];Z[1]:=XX.Z[2];IF XX.Z[2]<FMIN THEN
BEGIN FMIN:=XX.Z[2];XMIN:=XX.X[2];YMIN:=XX.Y[2] END;
X[3]:=XX.X[3];Y[3]:=XX.Y[3];Z[3]:=XX.Z[3];IF XX.Z[3]<FMIN THEN
BEGIN FMIN:=XX.Z[3];XMIN:=XX.X[3];YMIN:=XX.Y[3] END;
X[2]:=YY.X[3];Y[2]:=YY.Y[3];Z[2]:=YY.Z[3];IF YY.Z[3]<FMIN THEN
BEGIN FMIN:=YY.Z[3];XMIN:=YY.X[3];YMIN:=YY.Y[3] END;
END;
SIT[N+1]:=XX;SIT[N+2]:=YY;SIT[N+3]:=ZZ;
SIT[N].P:=MINOR(N);SIT[N+1].P:=MINOR(N+1);SIT[N+2].P:=MINOR(N+2);
SIT[N+3].P:=MINOR(N+3);DRAWTROJ(N);DRAWTROJ(N+1);DRAWTROJ(N+2);
DRAWTROJ(N+3);N:=N+3
END;
PROCEDURE SORT;
LABEL 2;
VAR Q:TROJ;M,I,L,K:INTEGER;
BEGIN MINMINOR:=1.0E30;M:=N-1;FOR I:=1 TO M DO BEGIN
L:=I;2:K:=L+1;IF SIT[L].P<SIT[K].P THEN BEGIN
Q:=SIT[K];SIT[K]:=SIT[L];SIT[L]:=Q;L:=L-1;
IF L>0 THEN GOTO 2 END;
END;IF SIT[N].P<MINMINOR THEN BEGIN MINMINOR:=SIT[N].P;
GOTOXY(2,2);WRITE('DOSAZENA PRESNOST:',FMIN-MINMINOR) END
END;
BEGIN WRITE('ZADEJ POCET TROJUHELNIKU:');FMIN:=1.0E30;MINMINOR:=1.0E30;II:=0;
;READLN(N);PLOCHA:=1.0E30;WRITE('ZADEJ PRESNOST:');READLN(EPS);JJ:=0;IJ:=0;
FOR I:=1 TO N DO BEGIN FOR J:=1 TO 3 DO WITH SIT[I] DO BEGIN
WRITE('BOD ',I:3,' X[',J:2,']= ','Y[',J:2,']= ');
READLN(X[J],Y[J]);Z[J]:=F(X[J],Y[J]) END;SIT[I].P:=MINOR(I);
END;SORT;
HIRES;DRAW(0,100,639,100,1);DRAW(319,0,319,199,1);FOR I:=1 TO N DO DRAWTROJ(I);
REPEAT II:=II+1;
ROZDEL;AREA(N);SORT;IF II>50 THEN BEGIN
NN:=1;FOR I:=1 TO N DO IF SIT[I].P>FMIN THEN NN:=NN+1;
IF NN<>1 THEN BEGIN FOR I:=NN TO N DO SIT[I-NN+1]:= SIT[I];N:=N-NN+1 END;
II:=0 END;
UNTIL (PLOCHA<EPS) OR (N>980); TEXTMODE(BW80);
WITH SIT[N] DO BEGIN
WRITELN(' R E S E N I :');
WRITELN('X=',XMIN,' Y=',YMIN);
WRITELN('Z=',FMIN) END;
WRITELN('POCET VYPOCTU FUNKCNICH HODNOT:',JJ);
WRITELN('POCET GENEROVANYCH OBLASTI:',IJ);
WHILE NOT KEYPRESSED DO;
END.
4.6. Dynamické programování.
Základní myšlenkou dynamického programování je převedení vícerozměrné optimalizační úlohy na posloupnost úloh menšího rozměru. Na rozdíl od matematického programování je těžké určit, pro které oblasti a třídy úloh je tento postup vhodný a rovněž není jednoduché popsat nějaké standardní schéma celého obecného řešení úlohy. Postup je nejjednodušší znázornit na úloze.
Příklad. n
Mějme následující
úlohu: Najděte minimum funkce m i n ![]() ci
* xi2
ci
* xi2
n i=1
při podmínkách : ![]() xi
= A , x > 0.
xi
= A , x > 0.
i=1
Úloha je ekvivalentní
následující úloze: n-1 m
i n ![]() ci
* xi2 i=1
ci
* xi2 i=1
při podmínkách n-1 ![]() xi
= A - xn , x > 0. i=1
xi
= A - xn , x > 0. i=1
Pokud označíme původní úlohu Fn (A) a novou Fn-1 (A - xn), můžeme řešení původní úlohy vyjádřit ve tvaru
m i n {cn * xn2 + Fn-1 ( A - xn ) }
0<xn<A
což je vlastně jednorozměrná úloha minimalizace. Tímto postupem jsme převedli řešení n-rozměrné úlohy na posloupnost řešení jednorozměrných optimalizačních úloh. Nalezení minima kvadratické funkce není obtížné. Vyřešme nyní konkrétní problém:
m i n {x12 + 2 * x22 + x32}
x1 + x2 + x3 = 9
Převedeme úlohu na požadovaný tvar
m i n {x12 + 2 * x22 + x32} = m i n {F2(9-x3) + x32}
x1 + x2 + x3 = 9 0<x3<9
Stejně můžeme postupovat s F2
F2(y1) = m i n {x12 + 2 * x22 }= m i n {F1(y1-x2) + 2 *x22}
x1 + x2 = y1, 0<x2<y1
F1(y2) = m i n {x12} x1 = y2
Nyní zpětným postupem dosazujeme a získáváme
F2(y1) = m i n {(y1-x2)2 + 2 *x22} 0<x2<y1
Řešení získáme klasicky derivací
x2(y1) = y1/3 ; F2 = ( 2 * y1)/3
dosadíme do původního prvního vztahu
F3 (9) = m i n {x32 + (2/3)*( 9 - x3)2 }.
Tuto úlohu řešíme stejně jako v předcházejícím případě a získáme
x3 = 3.6 x2 = 1.8 x1 = 3.6 .
Tento příklad sloužil spíše pro ilustraci metody. V praxi se dynamické programování používá spíše pro sekvenční rozhodování. Jedná se tedy o rozhodovací úlohy, kde hraje důležitou roli čas.
Zformulujme alespoň některé principy dynamického programování:
1. Výchozí úloha je vnořena do určité množiny optimalizačních úloh.
2. Množina řešení optimalizační úlohy je popsána jako funkcionální rovnice nebo jako soustava rovnic.
3. Řešení optimalizační úlohy je možné najít metodou zpětného průchodu.
4. Přechod při řešení
probíhá z jednoho stavu do druhého a
zachycuje
v sobě celou historii procesu.
Princip optimálnosti Bellmana:
Optimální strategie má tu
vlastnost, že bez ohledu na počáteční
podmínky
a řešení, je zbylé
řešení optimální
strategií pro stav, který vzniká po
prvním přechodu.