V dosavadních přednáškách jsme probírali jedno či vícekriteriální optimalizaci, ale v těchto úlohách byly předem pevně dané podmínky a ty se nijak neměnily v závislosti na našem roz­hodnutí. Také jsme uvažovali modely (rozhodování za rizika a nejistoty), kde nejsou podmínky pro rozhodování jisté, neboť závisí ještě na dalších okolnostech, o kterých nemáme jistotu, jak dopadnou.

Teorie her se zabývá rozhodováním v tzv. konfliktních situacích. Jedná se o situace, kdy okolí na naše rozhodnutí může nějakým způsobem zareagovat, udělat nějaké protiopatření, čímž se může zcela změnit naše situace.

Hlavní charakteristikou je, že zde není obecně jeden subjekt, který má v operaci svoje cíle, ale subjektů je víc a každý z těchto subjektů má svůj cíl. Variant je MOC. Přitom subjekt ani nemusí svůj skutečný cíl znát. Myslí si, že má jeden cíl, ale možná ve skutečnosti má cíl jiný…

Příklad:

Příkladem takové situace z ekonomie je oligopol. Pokud se bude rozhodovat jeden oligopolista sám a nebude brát v úvahu okolí, stanoví svůj objem výroby tak, aby maximali­zoval své tržby. Spočte si své jednotkové náklady závislé na objemu produkce, podle statistik dopočte, kolik bude jednotkový zisk v závislosti na objemu produkce dodávané na trh (uva­žuje, že na trh dodává sám) a odtud stanoví optimální výrobní plán.

 

Pokud nebude brát v úvahu ostatní oligopolisty a pokud i oni budou vyrábět, potom se cena na trhu sníží (není sám, kdo dodává zboží), a jeho zisky vůbec nemusí být, pro jím stanovený objem výroby, optimální.

Právě takovými situacemi se zabývá teorie her.

 

•   hra -  je operace, ve které operuje více stran (hráčů)

•   hráč – operující strana, účastník hry, který svým chováním může ovlivnit její výsledek; hráč může být buď racionální (usiluje o optimální výsledek hry) nebo indiferentní (výsledek hry je mu lhostejný)

•   strategie – množina prostředků, které má účastník operace (hry) k dispozici

•  Výhra, výplata hráče - kvantitativně vyjádřený výsledek hry, posuzovaný z hlediska uvažo­vaného hráče (kladná hodnota - užitek, záporná hodnota - škoda)

•  Cílová, výplatní funkce hráče - předpis pro výplatu v závislosti na zvolené strategii

·        podle počtu hráčů - hry 2 a n hráčů, kde n > 2

·        podle součtu výplat hráčů - hry s konstantním a hry s nekonstantním součtem; zvláštní případ hry s konstantním součtem je hra s nulovým součtem

·       podle velikosti prostoru strategií - hra konečná a nekonečná

·        podle informace - pokud hráči mají informace o dosavadních tazích protihráčů, ho­voříme o hrách s úplnou informací, pokud ne, potom o hrách s neúplnou informací

·        podle zájmů hráčů - hry antagonistické a hry neantagonistické; neantagonistické hry se dále člení na hry kooperativní a hry nekooperativní; v kooperativní hře lze vytvářet koalice nebo spíše to má smysl…

·      podle informací o důsledcích volby - hry deterministické; zvolíme-li strategii, víme přesně, kolik získáme a hry stochastické - do hry vstupuje náhoda, zvolíme- li strategii, výplata má nějaké pravděpodobnostní rozdělení

·    podle racionality hráčů - hry hrané podle minimaxu a hry hrané proti přírodě

Důležitou roli v teorii her mají konečné hry dvou hráčů s nulovým součtem, které nazý­váme maticové hry. Je to proto, že se hry dají zobrazit jako matice a pomocí takových prostředků se dají i matematicky řešit.

 

Abychom mohli naše teorie srozumitelně zapisovat, budeme používat následující (běžné) značení. Účastníky hry budeme značit písmeny A a B. Hru sledujeme z hlediska jednoho hráče, většinou z hlediska hráče A. Jeho výplata se nazývá výhra a výplata druhého hráče se nazývá prohra. Hráč A má k dispozici m strategiií a hráč B má k dispozici n strategií.

A ... prostor strategií prvního hráče

B ... prostor strategií druhého hráče

Ai ... i-tá strategie strategie prvního hráče, kde i = 1, 2, ...,m

Bj ... j-tá strategie druhého hráče, kde j = 1, 2,..., n

Všechny dvojice strategií A_i,Bj lze zapsat do matice typu m x n. Tato matice se nazývá výplatní maticí nebo maticí hry.

Pokud označíme prvky výplatní matice a_ij, platí a_ij = M\(A_i,Bj). Pak M\(A_i,Bj) je výplatní funkce hráče A. Výplatní funkce hráče B je M₂(A_i,Bj). Ve hře s nulovým součtem platí Mi(A_i,Bj) = -M₂(A_i,Bj), proto vystačíme se zápisem M(A_i,Bj)(viz dále). Hra je dána výčtem strategií jednotlivých hráčů a výplatními funkcemi. Smysl značení si ukážeme na následujících příkladech.

Příklad: Uvažujme hru o jednom tahu, ve které hráč A volí mezi dvěma čísly 1 a 2 a hráč B rovněž volí mezi dvěma čísly 1 a 2. Při výplatě dostává hráč A od hráče B 1 Kč v případě, jsou-li zvolená čísla různá a hráč A zaplatí 1 Kč hráči B v případě, že jsou tato čísla stejná. Výplatní matice hráče A je následující.

 

 

Příklad:

Předpokládáme, že slečna vlastní kožich, jehož hodnota je 5000 Kč. Může si tento kabát za 100 Kč pojistit a v případě, že jí bude kožich zničen požárem, bude jí škoda nahra­zena.

V této hře je jedním hráčem slečna a druhým „příroda". Strategie prvního hráče, tj. slečny jsou pojistit a nepojistit si kabát. Strategie „přírody" jsou kabát slečně shoří a nestane se s kabátem nic. Výplatní funkce slečny (u „přírody" nemají smysl) jsou podle ceny kabátu, ceny pojištění a ceny náhrady, kterou pojišťovna slečně poskytne. Pro slečnu můžeme napsat výplatní matici.

Výplatní matice slečny má tedy následující tvar:

 

V tomto příkladě je jeden hráč racionální (předpokládáme to o slečně) a jeden indiferentní. V tom případě se jedná o tutéž situaci jako v rozhodování za nejistoty.

 

Antagonistickým konfliktem rozumíme konflikt, kde proti sobě stojí dva racionální hráči a zisk jednoho hráče je roven ztrátě druhého hráče (př. sázky mezi dvěma lidmi). Nebo obecněji o co jeden získá více, o to druhý více ztratí (mají si nějakým způsobem rozdělit fixní částku). Lze říci, že takový typ konfliktu lze zapsat jako maticová hra hraná podle minimaxu. Cílem je maximální výhra hráče A a minimální prohra hráče B. Hra může mít řešení buď v ryzích nebo ve smíšených strategiích.

•   Čistá (ryzí) strategie - jedna z možných strategií hráče

Ryzí optimální strategii hráče A budeme značit A₀ a tato strategie přinese hráči A maximální výhru, ať již hráč B volí jakoukoliv strategii. Ryzí optimální strategii hráče B budeme značit B₀. Je to strategie, která zaručí hráči B minimální prohru, ať již hráč A volí jakoukoliv strategii. Pro strategie i = 1, 2, ...,m a j = 1, 2, ...,n platí

M(Ai, Bo) < M(Ao,Bo) < M(Ao, Bj)

Lze tedy říci, že jakýkoliv hráč si pohorší, pokud se odkloní od své optimální ryzí stra­tegie. Cena hry(v) je hodnota výplatní funkce M(A₀,B₀). Pokud je cena hry nulová, jedná se o hru spravedlivou, pokud není nulová, jedná se o hru nespravedlivou.

•   Smíšená strategie - náhodné střídání strategií hráče, přičemž je dáno rozdělení prav­děpodobnosti na prostoru ryzích strategií. Má smysl pouze u opakujících se her.

Výplata hráčů je zde náhodná veličina a její očekávanou hodnotu značíme E(x,y). Pokud volí hráči strategie nezávisle na sobě, pro očekávanou výhru platí

E(x, y) = £i£j- aijXiyj

Pro hráče A smíšenou strategii značíme x = [xi,x₂, ...,x_m] , smíšenou strategii hráče B značíme y = [y₁,y₂, ...,y_n] . Složky těchto vektorů jsou nezáporná čísla, jejichž součet je roven jedné. Ryzí strategie je pak zvláštním případem smíšené strategie, kdy jeden prvek je 1 a ostatní 0. Stejně jako u ryzích strategií, lze i zde zavést pojem optimální strategie, které budeme značit [x₀, y₀].

E(x, yo) < E(xo, yo) < E(xo, y)

Řešení hry v ryzích strategiích reprezentují tyto údaje: A₀,B₀,v, řešení hry ve smíšených strategiích reprezentují tyto údaje: x₀, y₀, v.

Matematickým modelem hry s konstantním součtem je M₁(A_ij,B_ij) + M₂(A_ij,B_ij) = k. My můžeme uvažovat hry se součtem nula, neboť všechny hry s konstantním součtem je možné převést na hry se součtem nula.

Máme-li konečný prostor strategií, tzv. konečnou hru, můžeme hru přepsat do matice A, kde řádky budou tvořit možné strategie prvního hráče a sloupce možné strategie druhého hráče. Prvek a_ij matice nám udává výplatu prvního hráče, pokud první zvolí ¿-tou strategii, tj. strategii A_i, a druhý hráč zvolí j-tou strategii, tj. strategii Bj. Protože se jedná o antago- nistický konflikt, potom je a_ij s opačným znaménkem, tj. -a_ij, výplatou druhého hráče, při stejných strategiích (viz výše). A tedy jedná se o tzv. jednomaticovou hru.

Poznámka: Všimněme si, že v této terminologii (uvažujeme ryzí strategie) tedy první hráč usiluje o maximalizaci:

max a_ij
ij

přičemž on může ovlinit pouze volbu i a volbu j ovlinit nemůže, kdežto druhý hráč usiluje o minimalizaci

                                                                                    min a_ij

                                                                                                                    ^j

kde druhý hráč může ovlinit volbu j, ale ne i.

Příklad: 

Uvažujme následující hru. Hrají dva hráči. Každý má pět sirek. Teď si každý může vzít do ruky kolik chce (z těch pěti sirek) a na povel ruce otevřou. Kdo bude mít v ruce více sirek, vyhrál, pokud mají stejně, je remíza.

Ze zadání příkladu je zřejmé, že je rozumné, aby každý hráč vzal do ruky všech pět sirek. Ukažme si, že stejně nám dovede poradit i teorie her.

Napišme si matici A výplatní matici prvního hráče a matici B výplatní matici druhého hráče. V obou maticích budou řádky odpovídat jednotlivým strategiím prvního hráče, po­stupně 1, 2,..., 5 sirkám v jeho ruce (předpokládejme, že musí alespoň jednu vzít) a sloupce steným způsobem jednotlivým strategiím druhého hráče. Výplatní matice mají tedy tvar:

Všimněme si, že skutečně platí A = - B, a tedy je zbytečné pro zápis takovéto hry používat dvě matice.

Hledáme-li optimální řešení antagonistického konfliktu, hledáme vlastně stabilní řešení. Sta­bilní v tom smyslu, že ani jednomu hráči se nevyplatí od této strategie „utéci", tj. má to být takové řešení, aby pokud pouze první hráč změní strategii a druhý hráč zůstane u své strategie, potom si první hráč pohorší. Stejně tak s druhým hráčem.

 

Strategie hráče A je maximinová, neboť hráč A předpokládá, že inteligentní B zvolí strategii, při níž je jeho prohra minimální a vybere si z těchto minimálních výher v řádcích maxima. Strategie, při které je toto maximum největší, je pro hráče A optimální. Této ma- ximinové strategii se říká také dolní cena hry. Strategie hráče B je minimaxová, neboť hráč B zjistí, kolik při každé strategii může prohrát nejvíce (maxima ve sloupcích) a z těchto největších proher vybere minimum. Tato minimaxová strategie se označuje jako horní cena hry.

Odtud vyplývá, že optimální řešení antagonistického konfliktu (v ryzích strategiích) exis­tuje, pokud platí:

min max a _ij = max min a _ij.                                                (1)

    j  i             i     j

Pokud je tato rovnost splněna, v matici existuje prvek, který je nejmenší ve svém řádku a největší ve svém sloupci. Tento prvek nazýváme sedlový bod.

Obrázek 1: Sedlový bod

Obecně matice mohou mít žádný, jeden nebo více sedlových bodů. Pokud nemají žádný, neexistuje optimální ryzí strategie, pokud mají jeden, určuje optimální strategii, pokud jich mají více, určují alternativní rovnovážné strategii.

Napišme si matici hry Kámen - nůžky - papír. Všimněme si, že nemá sedlový bod. Nee­xistuje tedy rovnovážné řešení v ryzích strategiích.

Pokud má alespoň jeden hráč nekonečně mnoho strategií, potom se jedná o tzv. nekonečnou hru.

Stejně jako ve vícekriteriálním hodnocení variant, i zde se můžeme setkat s tzv. dominovanými a nedominovanými variantami, resp. strategiemi.

Řekneme, že strategie A_k prvního hráče dominuje strategii A_l tohoto hráče, jestliže pro všechny možné strategie Bj druhého hráče platí, že

M(A_k, Bj) > M(Ai,Bj)

a zároveň existuje alespoň jedna strategie B_q taková, že

M(A_k,Bq) >M(Al,Bq).

Nebo-li pro jakoukoliv strategii druhého hráče platí, že výplata prvního hráče je při strategii

A_k větší nebo stejná než při strategii A_l a alespoň při jedné strategii je ostře lepší. Domino­vanost lze určit i u strategií hráče B.

Hráč A má možnost volit strategie A_1} A₂,..., A_m, hráč B má možnost volit mezi strategiemi B_1}B₂,..., B_n.

•  Je dána cena hry v, vektor x = [x₁,x₂,... ,x_m], pro jednotlivé složky tohoto vektoru platí Xi > 0 a J2^r_j=₁ Xi = 1. Vektor x je optimální strategií hráče A tehdy, když platí E(x, Bj) > v pro j = 1, 2,... ,n.

•  Je dána cena hry v, vektor y = [y₁,y₂,... ,y_n], pro jednotlivé složky tohoto vektoru platí yj > 0 a J2n₌₁ yj = 1. Vektor y je optimální strategií hráče B tehdy, když platí

E(A_i, y) < v pro i = 1, 2,... ,m.

•  Optimální strategie hráčů A a B ve hře s cenou v jsou x₀=[x₀₁,x₀2, ...,x_0m] a yo=[yoi,yo2, ...,yon]. Potom pokud:

a)  E(x₀, Bj) > v, platí y₀j = 0; 1 < j < n

b)   E(A_i, y₀) < v, platí x_0i = 0; 1 < i < m

c)   x_0i > 0, platí E(A_i, y₀)= v; 1 < i < m

d)  y₀j > 0, platí E(x₀, Bj)= v; 1 < j < n.

Tyto vztahy vyplývají ze vztahů mezi duálně sdruženými úlohami.

•  Pokud není optimální strategie hráče dána jednoznačně, každá konvexní kombinace optimálních strategií tohoto hráče představuje rovněž optimální strategii.

•  Jsou-li prvky a_ij výplatní matice A změněny o libovolnou konstantu k > 0, např. a_ij + k, ka_ij, těmto hrám odpovídají stejné optimální strategie. Cena hry je rovněž změněna o tuto konstantu. Jedná se o strategicky ekvivalentní hry. Startegicky ekvivalentní hru je možné získat i převodem hry s konstantním součtem na hru s nulovým součtem, popř. vynecháním dominovaných strategií (viz předchozí přednáška).

Výplatní matice hry je

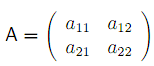
Tato hra nemá sedlový bod a my hledáme optimální smíšené strategie obou hráčů a cenu hry. Nejprve budeme určovat optimální smíšené strategie hráče A. Vzhledem k tomu, že hra nemá řešení v ryzích strategiích, obě složky vektoru optimální smíšené strategie hráče B musí být kladné. Neboli musí být splněny rovnosti a₁₁x₀₁ + a₂₁x₀₂ = v a a₁₂x₀₁ + a₂₂x₀₂ = v. Tyto dvě rovnice můžeme dále zapsat jako

aux01 + a21x02 = a^x01 + a22x02

Pokud vezmeme v úvahu, že x₀₁ +x₀₂ = 1, pak řešením soustavy dvou rovnic o dvou neznámých získáme následující řešení:

_x = ^a22 ^{- a}21 _x = ₀₁₁_₀₁₂ ⁰¹ aii + «22 - ai2 - a2i' ^{02 011}+⁰²² _⁰¹²_⁰²¹'

Po zjištění optimální strategie hráče A lze dopočítat i cena hry.

Nyní určíme optimální smíšenou strategi hráče B. Zde budeme vycházet z rovnosti

aiiyoi + ai2yo2 = a2iyoi + a22yo2

Opět vezmem v úvahu, že y_0i + y₀₂ = 1 a vyjádříme vztah pro výpočet optimálních smíšených strategií hráče B. Řešením je

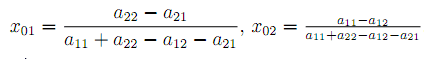
Příklad: 

Určete optimální smíšené strategie obou hráčů, znáte-li výplatní matice

Výsledky příkladu 1:

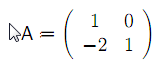
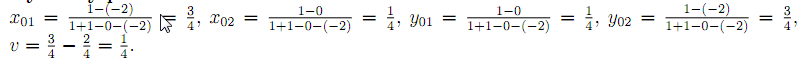
Grafické řešení maticových her

Pokud je hra m x 2 nebo 2 x n, lze ji řešit jednoduchým grafickým způsobem. Vzpomeňte na grafické odvozování velikosti koeficientu a u Hurwitzova přístupu při rozhodování za nejistoty. Do podobné soustavy souřadnic budeme zakreslovat prvky výplatní matice. Pokud budeme řešit hru 2 x n, na ose x budeme zjišťovat, jaké jsou smíšené strategie hráče A. Na osu v (kolmice na osu x v bodě 0) budeme vynášet číslo , které je ve výplatní matici na pozici 1, k, kde k = 12,..., n. Na osu z (kolmice na osu x v bodě 1) budeme vynášet číslo, které je ve výplatní matici na pozici 2k, kde k = 1, 2,... ,n. Oba body (prvky výplatní matice), příslušející jedné strategii hráče B, vždy spojíme přímkou. Když máme zakreslené všechny úsečky příslušející strategiím hráče B, hledáme část úsečky, pod kterou se nenachází body jiné úsečky. Tato část představuje graf minimální očekávané výhry hráče A. Pokud řešíme hry typu m x 2 vynášíme na souřadnoice v,z prohry hráče B při jednotlivých strategiích hráče A. Postup budeme ilustrovat na následujícíh příkladech.

Příklad 2: Mějme matici

•

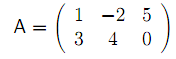Výsledky příkladu 2: x₀₁ = ii,x₀₂ = 11 ,v = 20. Grafické řešení viz obrázek 1. Příklad 3: Mějme matici

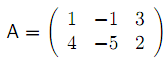
Výsledky příkladu 3: x₀₁ = 1,x₀₂ = 0,v = -1. Grafické řešení viz obrázek 2- Příklad 4: Mějme matici

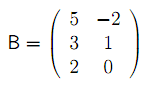
Výsledky příkladu 4: y₀₁ = 0,y₀₂ = 1,v = 1. Grafické řešení viz obrázek 3. Příklad 5: Mějme matici

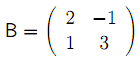
Výsledky příkladu 5: y₀₁ = 5,y₀₂ = 1 ,v = 5. Grafické řešení viz obrázek 4.

Mějme výplatní matici

 

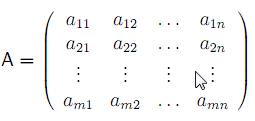
Následující soustavou nerovnic lze vyjádřit požadavek, aby optimální strategie hráče A tomuto hráči zajistila výhru nejméně v hodnotě ceny hry v, ať už hráč B volí jakoukoliv ze svých ryzích strategií:

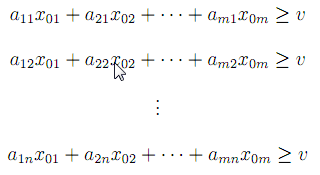
V případě, že matice obsahuje záporná čísla, ke všem jejím prvkům přičteme dostatečně velké kladné číslo. Tím získáme strategicky ekvivalentní hru, jejíž cena bude o přičítanou konstantu vyšší. Pokud je nezápornost prvků matice splněna, vydělíme cenou každou nerovnici soustavy a podíly ^ nahradíme symbolem t_i, pro i = 1, 2,... ,m. Soustava má pak tvar

Do podmínky Yh^r[L₁ X0i = 1 ^{za X}0i dosadíme součin vt_i. Potom platí

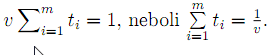
Danou úlohu můžeme zapsat jako úlohu LP. Na množině nezáporných řešení sou­stavy lineárních rovnic hledáme minimum lineární funkce f = T=\ t_i. Cena hry se rovná převrácené hodnotě účelové funkce a pro optimální strategii hráče A platí x_0i = vt_i pro i = 1, 2,... ,m. Potom platí

Nyní zformulujeme model z hlediska hráče B. Očekávaná prohra hráče B nesmí být větší než cena hry, ať už hráč A volí kteroukoliv ze svých ryzích strategií. Musí platit

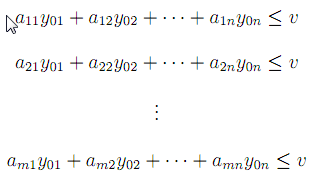
I u hráče B upravíme výplatní matici tak, aby cena hry byla kladná a položíme = ^sj ,j = 1, 2,... ,n. Soustavu pak můžeme napsat ve tvaru

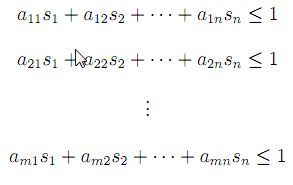
Do podmínky J2n=_i y₀j = 1 za y₀j dosadíme součin vSj. Potom platí

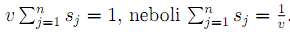
Snaha hráče A je minimalizovat cenu hry neboli maximalizovat součet n=_i Sj. Stejně jako u hráče A, i zde je možné úlohu zformulovat jako úlohu LP. Na množině nezáporných řešení soustavy lineárních nerovnic hledáme maximum lineární funkce z = J2¹j'=_i Sj.

Úlohy jsou duálně sdružené.

Příklad:Pro hru kámen - nůžky - papír zapíšeme výplatní matici (strategie jsou v pořadí kámen, nůžky, papír) a určíme optimální smíšené strategie pomocí LP.

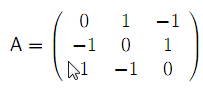
Výplatní matici upravíme přičtením čísla 1, aby matice neobsahovala záporná čísla.

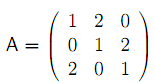
Z hlediska hráče A je model následující:

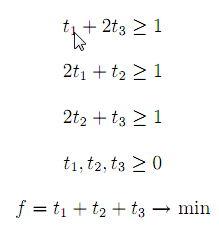
 Z hlediska hráče B je model následující:

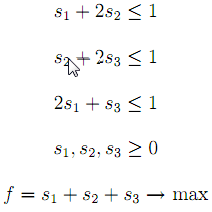
Výsledky pro A: 

t_i = i,t₂ = |,t₃ = i,f =1 ^ v' = 1,v = v' — 1 = 0 

Výsledky pro B:

s₁ = 3 ,s₂ = i ,s₃ = 3, z = 1 ^ v' = 1, v = v' — 1=0

 

Obrázek 2: Grafické řešení příkladu 2

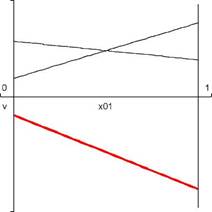
Obrázek 3: Grafické řešení příkladu 3

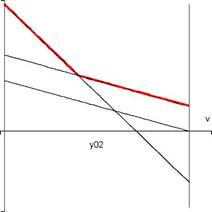
Obr8ázek 4: Grafické řešení příkladu 4

V tomto typu her hledáme optimální strategie hráče A, neboť hráč B (příroda) je indiferentní. S tímto přístupem jsme se již setkali u jednokriteriálního rozhodování za rizika a nejistoty.

•  můžeme předpokládat, že příroda je zákeřná a řešit hru podle principu minimaxu

•  můžeme hru řešit přístupy, které známe z rozhodování za nejistoty

 

 

Příklad:

 Výrobce vyrábí určité výrobky, z nichž některé mohou být vadné. Servisní organizace účtuje tomuto výrobci za záruční opravu 8 PJ/kus. Výrobce však může provést před expedicí výrobku kontrolu kvality (stoprocentně účinnou) a vadné výrobky ještě před expedicí opravit. Průměrné náklady na opravu jednoho výrobku před expedicí činí 4 PJ/kus a náklady na kontrolu činí 3 PJ/kus. Zisk z prodeje jednoho kusu výrobku činí 9 PJ/kus. Výrobce se rozhoduje, zda má dělat výstupní kontrolu.

Příklad 2: Majitel penzionu se má rozhodnout, jakou zásobu uhlí si má v létě udělat. Zná následující údaje:

 

Tyto ceny (v tisících Kč) odpovídají nákupu během zimy. V létě lze koupit uhlí za 6,0 tis.Kč za tunu, v domku je možnost uskladnit maximálně 6 tun. Uhlí, které po zimě zbyde, musí majitel odepsat. Jaká je optimální strategie tohoto majitele penzionu?

 

Obrázek 5: Grafické řešení příkladu 5

Při neantagonistickém konfliktu každý z hráčů sleduje své zájmy, které ovšem nemusí být v protikladu se zájmy svého protihráče. Jedná se o hry s nekonstantním součtem. Hráč A má opět možnost volit strategie A_l,A₂,... ,A_m, hráč B má možnost volit mezi strategiemi B_l, B₂,..., B_n. Výplatu hráče A při volbě strategií Ai,Bj značíme M_l(A_i, Bj). Výplata hráče B je M₂(A_i, Bj). U her s konstantním součtem bylo možné z výplaty jednoho hráče odvodit i výplatu protihráče. U neantagonistického konfliktu toto možné není, neboť platí

M_l(Ai, Bj) + M2(Ai, Bj) = konst.

Z tohoto důvodu je nutné pro každého hráče napsat matici jeho výplat. Tyto hry se proto nazývají dvojmaticové hry. Hry tohoto typu mohou být nekooperativní a kooperativní. Koo­perativní hry pak můžeme rozdělit na hry s přenosnou výhrou (hráči se dohodnou na rozdělení společné výhry) a na hry s nepřenosnou výhrou (hráči se dohodnou pouze na volbě strategií).

Nekooperativní hry

Tak jako u her s konstantním součtem jsme hledali optimální strategie hráčů, i v tomto typu her hledáme optimální strategie - zde hledáme Nashův rovnovážný bod. Tento bod reprezentuje dvojici strategií (A_q,B_q) - tzv. rovnovážné strategie.

Mi(Ai,Bo) < Mi(Ao,Bo)

M2(Aq, Bj) < M2(Ao,Bo)

U her s nekonstantním součtem si při odchýlení od optimální strategie hráč sám pohorší a může způsobit i zhoršení výplaty protihráče. U her s konstantním součtem hráč, který se odchýlil, zajistí protihráči vyšší výplatu.

Příklad 3: Uvažujme dva investory, kteří přemýšlejí o vstupu na trh ve třech různých odvětvích, ve kterých si mohou konkurovat. Každý z nich volí jedno odvětví, do kterého se rozhodne vstoupit, to znamená, nejprve si tam udělá reklamu a poté tam vstoupí. Tabulka uvádí zisky jednotlivých investorů v jednotlivém odvětví v případě, že tam vstoupí sami či oba.

 

Obecně zapíšeme jako matice A a B.

 

Pokusíme se najít Nashův rovnovážný bod, který se hledá následujícím způsobem:

•  V matici, reprezentující výplaty hráče A, nalezneme ve sloupcích maxima a příslušné dvojice zapíšeme do množiny Q.

•  V matici B najdeme maxima v řádcích a příslušné dvojice strategií zapíšeme do množiny R.

•  Vytvoříme průnik množiny Q a R (Q fl R), který představuje množinu rovnovážných bodů.

Je-li Nashův rovnovážný bod jeden, máme návod k optimálnímu jednání, není-li, nastává problém. Může se totiž stát, že každý hráč zvolí jiný, a potom se dostanou do oboustranně nevýhodné pozice.

V našem příkladu jsou dva rovnovážné body. Řešení je možné buď kooperací, nebo smíše­nými strategiemi.

V případě dvou rovnovážných bodů a více rovnovážných bodů ještě musíme rozlišit situace, kdy jeden rovnovážný bod pro oba hráče dominuje ostatní, potom tento bod dává návod na rovnovážné řešení.

Příklad 4:

 

Příklad 5:

 

Příklad 6:

 

Příklad 7:

 

Příklad 8:

 

Vězňovo dilema je model konfliktu, ve kterém obtížnost situace spočívá v tom, že obou­stranně výhodné řešení existuje, ale je nedostupné vzhledem k tomu, že jednostranné porušení solidárního jednání vede k podstatné výhodě pro toho, kdo porušil a k nevýhodě pro toho, kdo na oboustrannou solidárnost spoléhal.

 

Konflikt typu manželský spor se užívá pro modelování situace, kdy existuje více dvojic rovnovážných strategií, z nichž žádná není dominující. Například máme matici

 

V manželském páru má jeden zájem o kulturu a druhý o sport. Pokud se oba zúčastní kulturní akce, má nižší užitek hráč 2. Pokud se oba zúčastní sportovní akce, má nižší užitek hráč 1. Jestliže se hráči rozdělí, užitek každého z nich je ještě nižší (rozladění ze sporu mezi hráči).

V konfliktu typu kuřata se jedná o situace, kdy strany jednají tak, aby neztratily svou prestiž. Mějme např. dvojmaticovou hru

 

Každý z hráčů může buď ustoupit nebo neustoupit. Pokud oba hráči ustoupí, je výsledek neutrální, jednostranná ústupnost vede ke ztrátě prestiže toho, kdo ustoupil, oboustranná neústupnost vede ke krajně nepříznivým výsledkům u obou hráčů.

Pokud by hráčům dohoda přinesla větší výhry, je ji výhodné uzavřít. Hráči nejprve zjistí, kolik jsou schopni uhrát sami. Tyto výhry budeme značit v (A) a v(B). Buďto budeme a) maximalizovat zaručenou výhru, nebo budeme b) hledat rovnovážný bod. Ad a: Pro velikost výhry, kterou nemůže spoluhráč ohrozit platí:

v (A) = max» minj Mi(Aí, Bj) v(B) = maxj min» M₂(Aí, Bj) Pro maximální společnou výhru v(A,B) platí

v (A, B) = max^j [M₁(A_i, Bj) + M₂(A_t, Bj)], což je největší číslo v matici A a B. Dohoda se vyplatí uzavírat, pokud platí

v(A,B) > v (A) + v(B)

Další konflikt může nastat při dělení společné výhry. Částky, které dostanou hráči ze společné výhry, nejsou určeny jednoznačně a musí splňovat následující podmínku:

Pi + 6 = v(A,B),pi > v(A),£₂ > v(B). Pro rozdělení výher bylo stanoveno několik postupů.

1.   rozdělení na polovinu

_{p P} v(A,B) ^p1 = ^p2 = ~2~

2.   dělení v poměru přínosu hráčů ke společné výhře

pi : p2 = [v(A, B) - v(B)] : [v(A, B) - v(A)]

3.  každý hráč si vezme částku, kterou je schopen uhrát sám a o zbytek se dělí buď na polovinu nebo opět v poměru přínosů k výhře

Zde se sleduje odděleně výhra každého hráče v (A) a v(B). Ve dvoumatici pak hledáme čísla M₁(A_r,B_s) a M₂(A_r,B_s) tak, aby platilo

M₁(A_r,B_s > v(A),M₂(A_r,B_s) > v(B).

Pokud tato čísla existují, je výhodné alespoň pro jednoho hráče smlouvu o kooperaci, která by mu zajistila větší výhru, než kdyby hrál samostatně.

Modely oligopolu

Cournotův model

Předpokládejme, že v odvětví působí dvě firmy (duopol). Cournotův model vychází z předpokladů konkurence v objemu produkce. Objemy produkce výrobců:

q₁ - objem výroby prvního výrobce, q₂ - objem výroby druhého výrobce.

Cena produkce je funkcí celkového objemu produkce

p = g⁽qi + q2^

která je klesající, s růstem nabídky cena klesá.

Příjmová funkce i-té firmy je součinem objemu produkce této firmy a ceny

Ri(qi,q2) = pq%.

Mezní příjem udává změnu příjmu při jednotkové změně produkce

dRi(qi, q2)qi = g(qi, q2) + qidg(qi,q2)dqi = p + qidpdqi.

Nákladová funkce i-té firmy je rostoucí v závislosti na objemu produkce

Ci(qi).

Mezní náklady udávají změnu celkových nákladů v závislosti na jednotkové změně výroby. Zisková funkce i-té firmy závisí na chování obou firem

Zi(qi,q2) = pqi - Ci(qi)

Obě firmy se snaží maximalizovat svůj zisk vzhledem ke strategii konkurenta. Například druhá firma zvolí svoji strategii stanovením objemu výroby q₂°. První firma maximalizuje svůj zisk, který bude záviset na jejím objemu výroby i na objemu výroby druhé firmy. Pro dosažení maxima musí platit podmínka

dzi(qi,q2°)dqi = dRi(qi, q2°)dqi - dC1(qi)dqi = 0

Pokud druhá firma zvolí svoji strategii stanovením objemu výroby q₁°. Druhá firma maxima­lizuje svůj zisk, který bude záviset na jejím objemu výroby i na objemu výroby první firmy. Pro dosažení maxima musí platit podmínka

dz2(qi°,q2)dq2 = dR2(qi°,q2)dq2 - dC2(q2)dq2 = 0

Rovnovážný stav je určen dvojicí strategií q₁, q₂, které splňují zároveň bě podmínky. V rovno­vážném stavu je mezní příjem rovný mezním nákladům u obou firem. Z těchto rovnic můžeme odvodit funkce reakce chování duopolistů, která popisuje velikost produkce jednoho výrobce v závislosti na velikosti produkce druhého výrobce

qi = Vi⁽q2 ^),q2 = ^2⁽qi).

V Cournotově modelu obě se chovají obě firmy jako následníci, ani jedna z nich není v pozici vůdce.

Příklad: Cena produkce je dána funkcí

p =100 - (qi - q2).

Nákladové funkce obou firem jsou

Ci(qi) = 150 + 12qi, C2(q2) = q2²

 

Vychází ze stejných předpokladů, jako Cournotův, je jeho rozšířením. Jedna z firem je zde v pozici vůdce a druhá je v pozici následníka. Předpokládejme, že vůdcem je první firma, která stanoví svůj objem výroby q_i. Tato firma předpokládá, že druhá firma bude následníkem a určí svůj objem produkce podle funkce reakce

q2 = ^2⁽qi).

První firma maximalizuje svůj zisk

^zi = ⁽qi,q2⁾ = ^zi (qi^qi)),

což je funkce jedné proměnné q_i. Z podmínky pro maximum ziskové funkce = 0 dostaneme velikost objemu produkce vůdce. Z funkce reakce vypočteme velikost produkce následníka. Dosazením těchto čísel do cenové funkce získáme i rovnovážnou cenu.

Ve Stackelbergově modelu může být vždy jedna firma následníkem a jedna vůdcem, popř. obě firmy budou chtít být vůdci a toto vede ke Stackelbergově nerovnováze.

Příklad Budeme vycházet ze stejného zadání jako v předchozím případě a nejprve budeme uvažovat první firmu jako vůdce a druhou jako následníka.

Model kartelu Opět budeme uvažovat dvojici firem, jejichž objemy výroby značíme q_i,q₂. Cena je opět funkcí produkce, tato funkce je klesající. Nákladová funkce je rostoucí. Celkový zisk kartelu se vypočte podle vztahu

z(qi, q2) = p(qi + q2) - Ci(qi) - C2(q2).

Zisk je tedy funkcí objemu produkce obou duopolistů. Výrobní kvóty obou duopolistů, které maximalizují společný zisk, vychází z podmmínek

dzdq_i = 0, dzdq₂ = 0.

Zisk je potřeba rozdělit mezi oba duopolisty tak, aby žádná z firem nedopadla hůře než u Cournotova modelu.