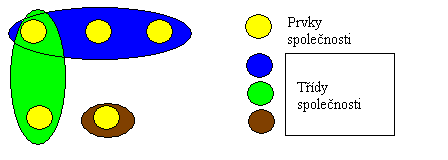3. Teorie grafů a úlohy na grafech.
Vědeckou disciplinu, kterou nazýváme teorií grafů, tvoří soubor poznatků
a metod, které vznikly především při zkoumání praktických úloh a byly později
doplněny a zobecněny. Z tohoto hlediska tedy teorie grafů ucelenou teorii
netvoří, ale je spíše pouze určitým souhrnem znalostí a pojmů.
Základy teorie grafů můžeme hledat v poměrně hluboké historii. Jednou z
nejznámějších je úloha, která vznikla někdy v 18.století v pruském městě
Königsbergu, jehož obyvatele zajímala odpověď na otázku: " Mohou-li
projít po uzavřeném okruhu ve městě tak, aby prošli všech sedm mostů a
to právě jednou?"
Situaci ve městě znázorňuje obr.1
Obr.1
Touto úlohou se zabýval i známý matematik Euler, jehož některé věty
si jistě pamatujete z matematické analýzy, který tuto úlohu nejen matematicky
zformuloval, ale i později sám vyřešil. Řešení této úlohy si ukážeme později.
Další důležitou etapou v rozvoji teorie grafů byla etapa spojená s řešením
matematické úlohy, která vznikla v 19.století v Anglii. Jedná se o poměrně
známou úlohu o čtyřech barvách:" Stačí čtyři různé barvy k vybarvení
libovolné zeměpisné mapy v rovině nebo na sféře tak, aby v této mapě nebyly
žádné dvě oblasti se společnou hranicí nenulové délky vybarveny stejnou
barvou?"
Na rozdíl od úlohy, kterou řešil Euler, byla tato úloha vyřešena
teprve v nedávno a to s využitím moderní výpočetní techniky. Že čtyři barvy
jsou nutné, je možné dokázat poměrně lehce:

Obr.2
V našem století prošla teorie grafů stadiem formování a po publikaci knihy
Königa v roce 1930 byla vpodstatě uznána jako samostatná disciplina. Obecně
je dnes teorie grafů součástí širší teorie, kterou nazýváme teorií společností.
3.1. Základní pojmy teorie společností a grafů.
Obecně je možné říci, že společnost i graf jsou určitými systémy, které
jsou charakterizovány obecně svými prvky a vztahy mezi nimi. Mějme zadánu
množinu prvků V = {v}, jejíž prvky budeme nazývat individui společnosti
a nechť je dále zadána množina U = {u : u E 2V} ,tuto množinu
nazýváme množinou tříd a je podmnožinou množiny všech podmnožin množiny
V .
Definice 3.1.
Společností nazýváme trojici {V,U,ľ}, kde ľ je tzv.incidenční
funkcí. Funkce každému prvku množiny U přiřazuje konkrétní podmnožinu
z množiny všech podmnožin množiny V.
Analogie s lidskou společností je zřejmá a odtud i název tohoto matematického
objektu. Uveďme si pro názornost příklad jedné takové společnosti. Nejprve
si jej zapíšeme matematicky a potom se jej pokusíme schématicky zobrazit:
V = {1,2,3,4,5 }, U = {{1,2,2},{3,4},{1,4,5},{5} }.Tímto zápisem
je již v množině U zahrnuta i incidenční funkce.
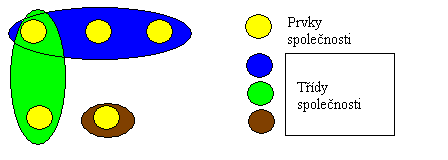
Obr.3
Definice 3.2.
Grafem nazýváme biparitní společnost.
Poznámka.
Biparitní společnost je taková společnost, ve které každý prvek třídy množin
U je dvouprvkovou množinou. Prvky množiny U nazýváme hranami
a prvky množiny V vrcholy grafu. Pokud v množinách vrcholů , které
jsou přiřazeny incidenční funkcí prvku množiny hran záleží na uspořádání,
pak graf nazýváme orientovaným. Na následujícím obrázku je zobrazen příklad
jednoduchého orientovaného grafu. V = {1 , 2 , 3 }; U = {u1 ,
u2 , u3 },dále je zadána incidenční funkce f(u1)={(1,2)};f(u2)=
{(3,2)};f(u3)={(1,3)}.
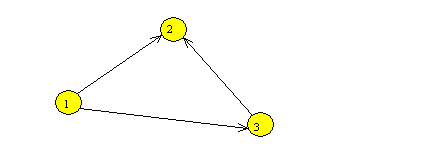
Obr. 4
Grafy zobrazujeme jako diagramy,schémata apod. Musíme si však uvědomit,
že rozmístění vrcholů a tvar spojení vrcholů nehraje vůbec žádnou roli
f stejný graf může být nakreslen nekonečně mnoha různými způsoby.
V následujícím odstavci budete seznámeni s některými základními pojmy teorie
grafů.
Definice 3.3
Vrchol grafu, který není incidentní s žádnou hranou se nazývá izolovaným
vrcholem. Vrchol, který je incidentní právě s jednou hranou je koncovým
vrcholem grafu.
Definice 3.4
Stupněm vrcholu (valencí) nazýváme počet hran, které jsou incidentní s
tímto vrcholem. Násobností hrany nebo dvojice vrcholů se nazývá počet hran,
incidentních s těmito vrcholy. Graf, ve kterém je násobnost hran vyšší
než jedna, se nazývá multigrafem.
V tomto grafu můžemeukázat některé z
těchto pojmů. Stupeň
vrcholu 1 je jedna,
vrcholu 2 je čtyři.
Vrcholy 1,3,4,5 jsou koncovými vrcholy grafu.
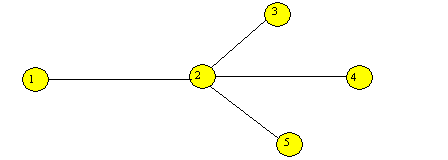
Obr. 5.
Definice 3.5
Cestou v grafu nazýváme posloupnost na sebe navazujících orientovaných
hran.Řetězcem nazýváme posloupnost na sebe navazujících hran grafu, bez
ohledu na orientaci.
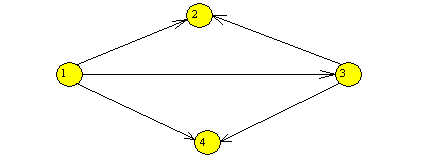
Obr. 6
V předchozím obrázku jsou cestami např. následující posloupnosti vrcholů:
1,3,2 ; 1,3,4 a řetězci posloupnosti 1,2,3,4 ; 2,3,1,4 apod.
Definice 3.6
Orientovaným cyklem nazýváme takovou cestu v grafu, která má identický
počáteční a koncový vrchol. Neorientovaným cyklem v grafu nazýváme řetězec,
který má stejný počáteční a koncový vrchol.
Na obrázku č.7 máme orientovaný cyklus 1,2,3,4, neorientovaný cyklus by
mohl být 4,3,2,1 apod.
Definice 3.7
Graf nazýváme souvislým, jestliže pro každé dva vrcholy existuje řetězec,
který je spojuje. Části nesouvislých grafů, které jsou samy o sobě souvislé,
se nazývají komponentami grafu. Souvislostí grafu nazýváme číslo, které
udává minimální počet vrcholů souvislého grafu, jejichž odstraněním vznikne
nesouvislý graf. Řezem grafu nazýváme číslo, které udává minimální počet
hran, po jejichž od@LH 6
stranění vznikne nesouvislý graf.
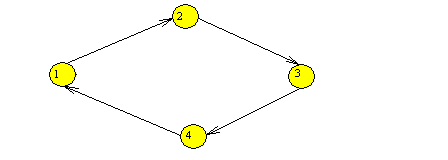
Obr. 7
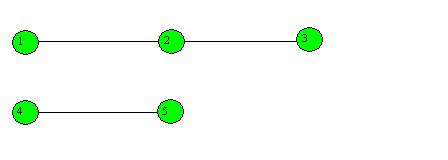 Obr. 8
Obr. 8
Graf zobrazený na obrázku 8 má dvě komponenty a jedná se tedy o nesouvislý
graf. Jeho souvislý podgraf , obsahující vrcholy 1,2,3 má souvislost 1
a řez také 1.
Definice 3.8
Stromem se nazývá souvislý graf, který neobsahuje ani jeden cyklus.
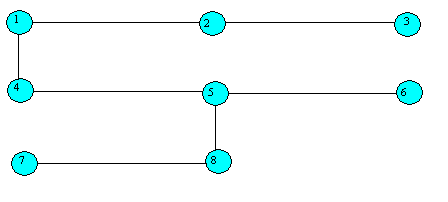
Obr. 9
Věta 3.1
Aby libovolný konečný, souvislý graf byl stromem, je nutné a postačující,
aby počet jeho hran byl o jednu menší než počet jeho vrcholů.
Důkaz.
Z definice stromu je zřejmé, že pokud ke stromu přidáme jednu jedinou hranu,
vznikne v takovém grafu cyklus, jestliže ze stromu odstraníme jednu jedinou
hranu, vznikne nesouvislý graf, jehož komponentami jsou dva stromy.
Proveďme nyní důkaz na základě těchto elementárních předpokladů. Využijme
k důkazu matematické indukce, kterou provedeme podle počtu vrcholů grafu.
Je zřejmé, že pro U =1 a V =2 věta platí. Předpokládejme
dále, že věta platí i pro libovolný počet vrcholů k,l < n. Podle
předpokladu matematické indukce jsou počty jejich hran k-1 a l-1.
Požadujme dále ,aby k+l=n+1.Grafy s těmito počty vrcholů jsou stromy
podle předpokladu. Přidejme nyní jednu hranu, kterou spojíme nějaký vrchol
prvního stromu s nějakým vrcholem druhého stromu. Vznikne nový souvislý
graf, který bude obsahovat n+1 vrchol, k-1+l-1+1=n hran. Současně je zřejmé,
že v grafu neexistuje cyklus, protože řezem nového grafu je číslo 1, jako
bylo i řezem každého ze dvou podgrafů, ze kterých jsme jej sestavovali.
Tím je věta dokázána.
Definice 3.9
Plochým (planárním) grafem se nazývá takový graf, který je možné zobrazit
v rovině tak, že žádné dvojice hran se nekřižují jinde než ve vrcholech.
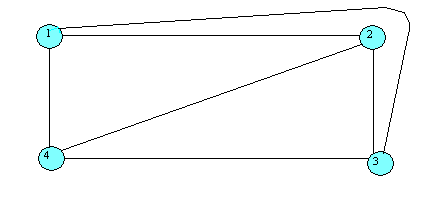
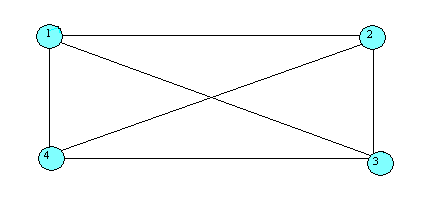 Obr. 10a a Obr. 10b
Obr. 10a a Obr. 10b
Na předcházejícím obrázku jsou dva identické grafy. Obrázek 10b je "neplanární"
graf a na obrázku 10a je tentýž graf nakreslen jako graf planární.
Definice 3.10
Pokrytím grafu se nazývá souvislý graf, který obsahuje všechny vrcholy
původního grafu a jehož množina hran je podmnožinou množiny hran původního
grafu.
Definice 3.11
Dva grafy G a H se nazývají izomorfními, právě když existuje
vzájemně jednoznačné zobrazení mezi množinami vrcholů a hran těchto grafů,
které zachovává vztah incidence.
( V tomto směru jsou grafy na obrázcích 10a a 10b izomorfní)
3.2 Eulerovy a Hamiltonovy cesty a cykly v grafech.
Vraťme se nyní zpět k problému úlohy o sedmi mostech. Po předešlém úvodu
nyní můžeme zformulovat tuto úlohu jako úlohu teorie grafů a také ji v
této teorii vyřešit.
Definice 3.12
Cestu v grafu, ve které se vyskytuje každá hrana právě jednou nazýváme
Eulerovou cestou. Má-li tato cesta počátek a konec v jednom jediném vrcholu,
pak se jedná o Eulerův cyklus v grafu.
Odpovídající graf naší úlohy je nakreslen na obrázku č.11.Vrcholy grafu
znázorňují jednotlivé ostrovy a pevniny a hrany jednotlivé mosty. Celý
problém se tedy transformoval do teoretické otázky, zda v tomto grafu existuje
Eulerova cesta. Odpověď by nás uspokojila pouze pro tento konkrétní případ
a to je málo. Euler vyřešil tuto otázku obecně a nutné a dostačující podmínky
pro existenci Eulerovy cesty v grafu formuluje následující věta.
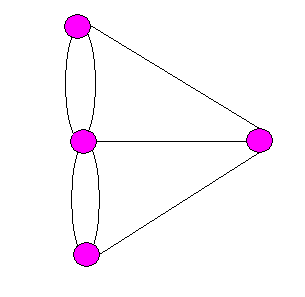
Obr. 11
Věta 3.2
Eulerova cesta v souvislém grafu existuje, právě když tento graf obsahuje
maximálně dva vrcholy lichého stupně.Předpokládáme, že graf je konečný.
(Na základě této věty můžeme konstatovat, že graf nakreslený na obrázku
8 takovouto cestu neobsahuje.)
Důkaz.
Důkaz provedeme konstruktivně, to znamená, že současně ukážeme, jak takovou
cestu najít. Dříve než přejdeme k důkazu, konstatujme, že souvislý graf
má buď všechny vrcholy sudého stupně, nebo dva nebo více vrcholů lichého
stupně. Jinými slovy neexistuje graf s právě jedním vrcholem lichého
stupně.
Předpokládejme nejprve, že graf obsahuje právě dva vrcholy lichého stupně.
Označme je jako vrcholy A a B. Začněme sestavovat cestu z
vrcholu A tak,že se budeme pohybovat z tohoto vrcholu po neopakujících
se hranách tak dlouho, dokud to bude možné (možné to bude do té doby, dokud
neskončíme ve vrcholu B a to proto, že všechny ostatní vrcholy mají
sudý stupeň a tedy jestliže do vrcholu po jedné hraně vejdeme - tu již
nemůžeme použít - zbyde minimálně jedna hrana, po které uvedený vrchol
můžeme opustit), cestu ukončíme ve vrcholu B. Nyní mohou nastat
dvě varianty - prošli jsme všechny hrany grafu a pak je Eulerova cesta
nalezena
- zůstaly hrany, kterými jsme neprošli, všechny zbylé vrcholy s neprojitými
hranami mají sudý stupeň.
V prvém případě je věta dokázána. Ve druhém případě odstraníme z grafu
všechny použité hrany a získáme podgraf, ve kterém má každý vrchol sudý
stupeň. Protože podle předpokladu je graf souvislý, musí se najít takový
vrchol C ,který leží na již námi nalezené cestě a je incidentní
nějakým hranám nového grafu. Vyjdeme-li z tohoto vrcholu C po nějaké
hraně (po vyjití bude mít tento vrchol jako jediný lichý stupeň v novém
grafu), musíme se do něj opět vrátit a vytvoříme tedy vlastně v tomto novém
grafu Eulerův cyklus. Cestu v původním grafu získáme jako sjednocení cesty
A-C,C-C,C-B. Znovu mohou vzniknout nám již známé dvě varianty. Tímto
způsobem můžeme pokračovat až do vyčerpání všech hran grafu. Je zřejmé,
že tento proces je konečný. Pokud mají všechny vrcholy sudý stupeň je možno
vynechat první část důkazu a začít od vrcholu C. V případě všech
vrcholů sudého stupně existuje tedy v grafu Eulerův cyklus. Věta je dokázána,
co se týče dostatečnosti. Z hlediska nutné podmínky je důkaz triviální.
Pokud by v grafu existovaly více než dva vrcholy lichého stupně, musela
by mít cesta víc než jeden začátek nebo víc než jeden konec, což je zřejmý
nesmysl.
Praktickými úlohami na tento problém jsou úlohy o svozu odpadu z městských
ulic, stanovení trasy pro čištění vozovek apod. Zajímavou úlohou je také
úloha o výběru ulic s jednosměrným a obousměrným provozem, kdy je jednosměrný
provoz žádoucí realizovat v maximálním počtu ulic.
Definice 3.13
Prostý cyklus je takový cyklus v grafu, který prochází každým vrcholem
cyklu pouze jednou.
Definice 3.14
Graf se nazývá grafem Hamiltona, jestliže obsahuje prostý cyklus, který
obsahuje všechny vrcholy grafu.
Definice 3.15
Graf, který obsahuje pro libovolnou dvojici vrcholů jim incidentní hranu,
se nazývá plným grafem.
Věta 3.3
Plný graf je vždy grafem Hamiltona.
Důkaz.
Plný graf je charakteristický tím, že obsahuje spojnice libovolných dvou
vrcholů. Je zřejmé, že pokud vyjdeme z vrcholu s číslem 1, můžeme
se po nějaké hraně dostat do každého z n-1 zbylých vrcholů, z druhého
pak do všech n-2 vrcholů, v kterých jsme ještě nebyli a podobně
dál. Z vrcholu s číslem n pak zpět do prvního vrcholu a tím je věta
dokázána.
Je zajímavé, že předchozí věta dává postačující podmínku pro existenci
Hamiltonova cyklu. Na rozdíl od Eulerovy věty nutná podmínka pro existenci
cyklu Hamiltona v grafu není známa.
Aplikační úlohou pro nalezení nejkratšího cyklu Hamiltona v grafu je známá
úloha o obchodním cestujícím, která se formuluje následovně:
Je dáno m míst, která má navštívit obchodní cestující.
Cestující vyjíždí z jednoho z těchto míst , opět se do něj musí vrátit
a má navštívit všech m míst právě jednou. Cílem operace přitom
je, aby jeho cesta byla co nejkratší.
Jinými slovy je v oblasti teorie grafů zadána úloha o nalezení nejkratšího
cyklu Hamiltona. Algoritmem (jedním z nejefektivnějších) pro řešení této
úlohy se zabývá paragraf 3.4.
3.3 Algebraická vyjádření grafů.
Jedním z důležitých směrů teorie grafů bezesporu souvisí s metodami jejich
popisu. Jak jsme si již ukázali,jeden graf můžeme nakreslit různými způsoby,kdežto
matematické vyjádření grafu určitými prostředky je pouze jedno.
Druhým důvodem pro algebraický popis grafů je zpracování úloh teorie grafů
na počítači - schéma si zatím počítač dostatečně rychle a srozumitelně
nepřečte.
Grafy popisujeme obvykle prostřednictvím vektorů a matic, používáme tedy
matematický aparát lineární algebry. Díky tomu můžeme pak s grafy provádět
různé algebraické operace a jejich výsledky opět zpětně interpretovat v
teorii grafů.
Incidenční matice grafu.
Incidenční matice, neboli česky matice sousednosti, zachycují matematicky
vztahy sousednosti vrcholů, hran a vrcholů a hran. Nejčastěji, mohou ale
zachycovat i sousednost cyklů apod.
a) matice sousednosti vrcholů grafu. Prvky této matice jsou čísla
0 nebo 1 u grafu a obecně celá čísla u multigrafu. Prvek matice aij
je roven počtu hran vedoucích z vrcholu i do vrcholu j grafu
(u neorientovaného grafu pouze počtu hran, které spojují vrcholy i a
j). Matice je čtvercová, řádky a sloupce odpovídají vrcholům grafu.
Pokud je graf neorientovaný, je matice symetrická.
b) matice sousednosti hran grafu. V této matici řádky a sloupce
odpovídají hranám grafu a každý prvek matice aij je roven počtu
vrcholů, které jsou incidentní hranám i a j.
c) matice sousednosti vrcholů a hran. V této matici řádky odpovídají
vrcholům grafu a sloupce hranám. Prvek matice je roven jedné (nule), když
odpovídající vrchol je (není) incidentní odpovídající hraně.
d) matice vzdáleností vrcholů grafu. V praxi se velmi často setkáváme
s reálnými grafy a sítěmi,jako jsou silniční, železniční, dopravní, energetické
aj. V těchto případech pouze topologie je grafu slabou charakteristikou
reálné úlohy, a proto do modelu vnášíme další doplnitelné informace. Jednou
z těchto informací může být vzdálenost mezi vrcholy. Tuto otázku řešíme
tak, že každé hraně grafu přiřadíme ještě číselnou hodnotu (její délku).
Takový graf pak nazýváme ohodnoceným grafem.
Vrcholy takovéto matice odpovídají sloupcům i řádkům a prvky této matice
pak vzdálenostem odpovídajících vrcholů grafu.
Příklad.
Pro ilustraci a lepší pochopení výše uvedených pojmů si zobrazme určitý
graf a vytvořme jeho incidenční matice. Graf je znázorněn na obrázku č.12.
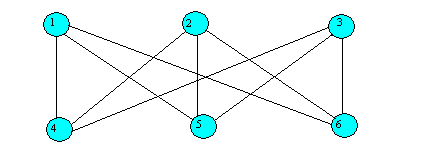
Obr. 12
Incidenční matice vrcholů grafu
| 0
|
0
|
0
|
1
|
1
|
1
|
| 0
|
0
|
0
|
1
|
1
|
1
|
| 0
|
0
|
0
|
1
|
1
|
1
|
| 1
|
1
|
1
|
0
|
0
|
0
|
| 1
|
1
|
1
|
0
|
0
|
0
|
| 1
|
1
|
1
|
0
|
0
|
0
|
Incidenční matice hran grafu
| 2
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
| 1
|
2
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
| 1
|
1
|
2
|
0
|
0
|
1
|
1
|
0
|
0
|
| 1
|
0
|
0
|
2
|
1
|
1
|
0
|
0
|
1
|
| 0
|
1
|
0
|
1
|
2
|
1
|
0
|
1
|
0
|
| 0
|
0
|
1
|
1
|
1
|
2
|
1
|
0
|
0
|
| 0
|
0
|
1
|
0
|
0
|
1
|
2
|
1
|
1
|
| 0
|
1
|
0
|
0
|
1
|
0
|
1
|
2
|
1
|
| 1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
2
|
Incidenční matice vrcholů a hran grafu.
| 1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
| 0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
| 0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
| 1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
| 0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
| 0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
Příklad.
Uveďme si nyní příklad ohodnoceného grafu a odpovídající matice vzdáleností
tohoto grafu.
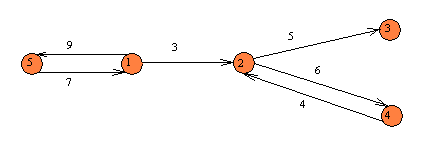
Obr.13
| 0
|
3
|
#
|
#
|
7
|
| #
|
0
|
5
|
6
|
#
|
| #
|
#
|
0
|
#
|
#
|
| #
|
4
|
#
|
0
|
#
|
| 9
|
#
|
#
|
#
|
0
|
V uvedené matici symbol nekonečno znamená, že mezi uvedenými vrcholy chybí
přímá spojnice.
3.4 Metoda větví a hranic, algoritmus Littla.
Metoda větví a hranic je v současné době jednou z nejefektivnějších optimalizačních
metod, zejména pro úlohy kombinatorického typu. Její podstatou je rozdělení
oblasti přípustných řešení (to jsou taková řešení, která vyhovují
omezujícím podmínkám úlohy - v našem případě jsou přípustnými řešeními
všechny cykly Hamiltona) na několik částí, obvykle na dvě. Pokud se jedná
o úlohu minimalizační, pak nalezneme na každé z těchto částí minorantu,
což je taková funkce, která je na celé části množiny přípustných řešení
menší než původní cílová funkce úlohy. Dále větvíme tu část množiny přípustných
řešení, která má menší minorantu (předpokládáme, že je více pravděpodobné,
že hledané optimální řešení je v této části). Odtud tedy část názvu metody
- metoda větví. Pokud se nám podaří nalézt tímto postupem nějaké řešení
(části množiny se neustále zmenšují až v nich může zbýt pouze jeden bod),
pak z řešení vyloučíme všechny množiny, které vznikly větvením a jejichž
minoranta je větší než hodnota cílové funkce na nalezeném řešení (protože
podle definice minoranty se v této množině nemůže vyskytovat řešení, které
by bylo lepší, než řešení námi již nalezené). U zbylých množin pokračujeme
v procesu dělení do té doby, dokud je co dělit.
Jinými slovy, nalezené řešení tvoří jakousi hranici, podle které
oddělujeme množiny na perspektivní a neperspektivní. Toto je současně popis
metody a zdůvodnění jejího názvu.
Algoritmus Littla.(Základní myšlenky)
KROK 1. Zadáme matici vzdáleností grafu. V této matici neexistující hrany
nahradíme symbolem .Dále provedeme redukci matice sazeb, to znamená, že
od každého prvku v řádku odečteme nejmenší prvek v tomto řádku a od každého
prvku ve sloupci potom odečteme také nejmenší prvek v tomto sloupci. Vznikne
nezáporná matice vzdáleností, která má tu vlastnost, že optimální řešení
původní úlohy je stejné, jako řešení nové úlohy s touto redukovanou maticí
sazeb.
Nechť cij je prvek matice sazeb. V takovém případě pak cílovou funkci,
která minimalizuje délku cyklu Hamiltona, můžeme vyjádřit jako
m i n 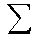
 cij*xij
= >
cij*xij
= > 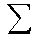
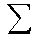 (cij - ai - bj)*xij =
(cij - ai - bj)*xij =
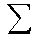
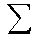 cij*xij
-
cij*xij
- 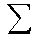 ai * (
ai * (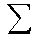 xij) -
xij) - 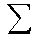 bj *
(
bj *
(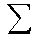 xij) =
xij) =
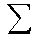
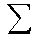 cij*xij - A - B ,
cij*xij - A - B ,
to znamená, že původní a nová cílová funkce se mezi sebou liší pouze o
konstantu a tedy z hlediska argumentu mají stejné optimální řešení. Pokud
nyní sečteme prvky ai a bj , které vznikaly při redukci matice
vzdáleností
ľ = 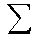 ai +
ai + 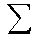 bj,
bj,
dostaneme konstantu, která je minorantou a říká nám, že v grafu neexistuje
žádný cyklus Hamiltona, který by byl kratší než výše uvedená hodnota. Matice,
která vznikne redukcí matice původní, má tu vlastnost, že v každém řádku
a každém sloupci je minimálně jedna nula. Pokud by se nám podařilo vybrat
v každém sloupci a řádku právě jednu nulu, pak bychom získali cyklus Hamiltona
a jeho délka by byla rovna minorantě. Protože tato situace je poměrně málo
pravděpodobná, je třeba určit pravidlo, podle kterého vybereme nějakou
z perspektivních nul a rozvětvíme množinu všech cyklů Hamiltona na dvě
skupiny. Na ty, které danou, perspektivní hranu obsahují, a na ty, které
tuto hranu neobsahují. Pro tento účel si jednotlivé nuly ohodnotíme tzv.
stupni, což jsou čísla, která udávají , co ztrácím, pokud uvedenou nulu
vyberu. Stupeň nuly tvoří součet dalšího minimálního prvku ve sloupci a
v řádku.
KROK 2. Vypočteme stupně jednotlivých nul v redukované matici.
oij = min cil + min ckj ,pro všechna cij=0
Nyní vybereme takovou nulu, pro kterou je stupeň maximální. Pokud je takových
nul více, vybereme některou z nich. Nechť je to nula s indexy r,s.
KROK 3. Rozdělíme množinu všech cyklů Hamiltona na dvě disjunktní podmnožiny.
Na podmnožinu, která obsahuje cykly s hranou (r,s) a na podmnožinu,
ve které žádný cyklus Hamiltona neobsahuje tuto hranu. V algebraickém vyjádření
toho dosáhneme tak, že v prvém případě vyškrtneme z matice vzdáleností
řádek r a sloupec s a prvek csr zaměníme za nekonečno,
nekonečnem nahradíme také všechny prvky, které by mohli tvořit kratší cykly
( tím eliminujeme vznik jiných cyklů, než jsou cykly Hamiltona). Ve druhém
případě zaměníme pouze prvek crs za nekonečno (tím dosáhneme toho,
že cyklus, který by obsahoval tuto hranu, má nekonečnou délku a tedy nemůže
být minimální). Takto tedy vznikly z původní matice dvě matice nové. Označme
je X0 a X1.
KROK 4. Nyní provedeme redukci matic X0 a X1 a vypočteme
hodnoty minorant těchto matic jako
ľ0 = ľ + h0 a ľ1 = ľ + h1 ,
kde h0 a h1 jsou minoranty těchto dvou nových matic. Nyní
z těchto dvou matic vybereme tu, která má menší minorantu a podrobíme ji
krokům 2,3 algoritmu. Dostaneme se znovu ke kroku 4, ale již se třemi maticemi
např. X00,X01,X1, vypočteme minoranty matic ľ01,ľ00
a z těchto tří minorant (ještě máme minorantu ľ1) vybereme minimální.
Takto postupujeme do té doby, dokud nedostaneme matici ,jejíž hodnost se
rovná dvěma (Rank Xijkl..= 2). V takovém případě již máme nalezen
jeden z cyklů Hamiltona (zbylé dvě hrany leží buď na hlavní nebo na vedlejší
diagonále této matice). Známe-li nějaký cyklus Hamiltona, můžeme potom
odstranit všechny množiny Xijkl.., jejichž minoranty jsou větší
nebo rovny délce našeho cyklu. Pokud jsme takto odstranili všechny matice
Xijkl..,pak můžeme celý postup algoritmu ukončit a námi nalezený
cyklus bude minimálním cyklem Hamiltona v grafu. Pokud se nám nepodařilo
odstranit všechny matice, pak pokračujeme ve větvení té, která má minimální
minorantu.
Celý postup si ukážeme na konkrétním příkladu. Nechť je zadán graf maticí
vzdáleností
|
|
|
|
|
|
ai
|
| #
|
30
|
40
|
15
|
6
|
9
|
| 10
|
#
|
18
|
7
|
9
|
7
|
| 20
|
30
|
#
|
1
|
10
|
1
|
| 25
|
10
|
35
|
#
|
5
|
5
|
| 9
|
8
|
7
|
6
|
#
|
6
|
po odečtení hodnot ai od jednotlivých řádků vznikne následující
matice
| #
|
24
|
34
|
9
|
0
|
|
| 3
|
#
|
11
|
0
|
2
|
|
| 19
|
29
|
#
|
0
|
9
|
|
| 20
|
5
|
30
|
#
|
0
|
|
| 3
|
2
|
1
|
0
|
#
|
|
| 3
|
2
|
1
|
0
|
0
|
bj
|
Odečtením hodnot bj od příslušných sloupců vznikne redukovaná matice
vzdáleností a sečtením hodnot ai a bj hodnota minoranty ľ.
| #
|
22
|
33
|
9
|
0
|
| 0
|
#
|
10
|
0
|
2
|
| 16
|
27
|
#
|
0
|
9
|
| 17
|
3
|
29
|
#
|
0
|
| 0
|
0
|
0
|
0
|
#
|
ľ = 6 + 7 + 1 + 5 + 6 + 3 + 2 + 1 + 0 + 0 = 31
Nyní můžeme konstatovat, že neexistují žádné cykly Hamiltona, které by
měly menší délku než 31 jednotek. Najdeme nyní stupně jednotlivých nul.
| #
|
22
|
33
|
9
|
0-9
|
| 0-0
|
#
|
10
|
0-0
|
2
|
| 16
|
27
|
#
|
0-9
|
9
|
| 17
|
3
|
29
|
#
|
0-3
|
| 0-0
|
0-3
|
0-10
|
0-0
|
#
|
Jak vidíme , jako nejperspektivnější se jeví prvek matice (5,3), což odpovídá
hraně 5,3 grafu. Vytvoříme nyní matice X0 a X1.
| #
|
22
|
9
|
0
|
| 0
|
#
|
0
|
2
|
| 16
|
27
|
0
|
#
|
| 17
|
3
|
#
|
0
|
|
|
3
|
|
|
Znovu musíme provést redukci matice sazeb a vypočíst minorantu, která pro
tuto matici nyní bude
ľ0 = 31 + 3 = 34
Dále vytvoříme matici X1
| #
|
22
|
33
|
9
|
0
|
| 0
|
#
|
10
|
0
|
2
|
| 16
|
27
|
#
|
0
|
9
|
| 17
|
3
|
29
|
#
|
0
|
| 0
|
0
|
#
|
0
|
#
|
|
|
|
10
|
|
|
ľ1 = 31 + 10= 41
Z vypočtené minoranty vidíme, že minoranta první matice je nejmenší, a
proto budeme dále větvit matici X0. Vypočteme nové stupně nul:
| #
|
19
|
|
9
|
0-9
|
| 0-0
|
#
|
|
0-0
|
2
|
| 16
|
24
|
|
0-16
|
#
|
| 17
|
0-19
|
|
#
|
0-3
|
|
|
|
|
|
|
Největší stupeň má nula pro prvek 2,4. Podle tohoto prvku tedy rozvětvíme
matici dále
| #
|
19
|
|
9
|
0
|
| 0
|
#
|
|
0
|
2
|
| 16
|
24
|
|
0
|
#
|
| 17
|
3
|
|
#
|
0
|
|
|
|
|
|
|
Vypočteme znovu minoranty pro tyto dvě matice a sice
ľ00 = ľ0 = 34 , ľ01= ľ0 + 19 = 53 , ľ1
= 41 ,
odtud je zřejmé, že budeme dále větvit množinu X00. Pro tento účel
opět vypočteme stupně jednotlivých nul.
| #
|
|
|
9
|
0-11
|
| 0-16
|
|
|
#
|
2
|
| 16
|
|
|
0-25
|
#
|
|
|
|
|
|
|
|
|
|
|
|
|
Po rozvětvení podle hrany 3,4 získáme následující dvě matice. První má
minorantu stejnou jako matice předchozí, druhá má minorantu 59.
ľ000=ľ00=34 , ľ001=ľ00+25=59 ,ľ01= ľ0
+ 19 = 53 , ľ1 = 41 .
Je vidět, že nejmenší minorantu má první množina. V ní můžeme už nyní určit
cyklus Hamiltona, který tvoří dříve vybrané hrany (5,3),(4,2),(3,4) a dvě
hrany z poslední množiny (1,5) a (2,1). Délka tohoto cyklu Hamiltona je
34 jednotek. Další postup algoritmu je zbytečný, protože žádná ze zbylých
množin nemá menší minorantu než je délka tohoto cyklu, a proto v nich nemůže
být obsažen kratší cyklus. Je třeba však mít na paměti,že tato situace
může reálně nastat a pak je třeba se vrátit k větvení této množiny!!!
Zamyslete se nad úlohou, kdy není třeba se vrátit zpět do výchozího vrcholu
grafu a nad úlohou, kdy je naopak pevně určen počátek cesty obchodního
cestujícího.
Výše uvedený algoritmus realizuje následující program.
(tento program neeliminuje všechny kratší cykly)
PROGRAM LITTLE;
LABEL 9;
CONST MAX=10;MUCH=32767;
TYPE UKAZ=^ZAZNAM;
MATRIX=ARRAY[1..MAX,1..MAX] OF INTEGER;
ZAZNAM=RECORD
MAT:MATRIX;
GAMA,ROZMER:INTEGER;
NEXT:UKAZ
END;
VAR X,ZACATEK:UKAZ;
POLE:ARRAY[1..8] OF INTEGER;
A,M:MATRIX;
G,R,U,V,I,J,N,SUM,C:INTEGER;
SB:STRING[14];
F:TEXT;
FUNCTION MIN(L:INTEGER;HORZ,SELF:BOOLEAN):INTEGER;
VAR K,MM:INTEGER;
BEGIN MM:=MUCH;CASE HORZ OF
TRUE :FOR K:=1 TO N DO
IF (A[L,K]>=0) AND (A[L,K]<MM) AND ((L<>I) OR (K<>J) OR
SELF)
THEN MM:=A[L,K];
FALSE:FOR K:=1 TO N DO
IF (A[K,L]>=0) AND (A[K,L]<MM) AND ((K<>J) OR (L<>I) OR SELF)
THEN MM:=A[K,L]
END;IF MM>32700 THEN MIN:=0 ELSE MIN:=MM
END; (* MIN *)
PROCEDURE REDUC;
VAR S:INTEGER;
BEGIN SUM:=0;
FOR I:=1 TO N DO
BEGIN S:=MIN(I,TRUE,TRUE);
IF S>0 THEN FOR J:=1 TO N DO IF A[I,J]>=0 THEN A[I,J]:=A[I,J]-S;
SUM:=SUM+S
END;
FOR J:=1 TO N DO
BEGIN S:=MIN(J,FALSE,TRUE);
IF S>0 THEN FOR I:=1 TO N DO IF A[I,J]>=0 THEN A[I,J]:=A[I,J]-S;
SUM:=SUM+S
END
END; (* REDUC *)
PROCEDURE ZARAD;
VAR P,Q:UKAZ;
BEGIN P:=ZACATEK;Q:=NIL;
WHILE (P^.GAMA<G+SUM) OR (P^.GAMA=G+SUM) AND (P^.ROZMER<R) DO
BEGIN Q:=P;P:=P^.NEXT END;
NEW(X);X^.GAMA:=G+SUM;X^.MAT:=A;X^.ROZMER:=R;
IF Q=NIL THEN
BEGIN X^.NEXT:=ZACATEK;ZACATEK:=X END
ELSE BEGIN X^.NEXT:=P;Q^.NEXT:=X END
END; (* ZARAD *)
BEGIN WRITE('Nazev datoveho souboru:');READLN(SB);ASSIGN(F,SB);
RESET(F);READLN(F,N);
FOR I:=1 TO N DO
BEGIN FOR J:=1 TO N DO BEGIN READ(F,A[I,J]);WRITE(LST,A[I,J]:7) END;
READLN(F);WRITELN(LST) END;WRITELN(LST);WRITELN(LST);
REDUC;G:=SUM;R:=N; FOR I:=1 TO 8 DO POLE[I]:=0;
NEW(ZACATEK);ZACATEK^.NEXT:=NIL;ZACATEK^.GAMA:=MUCH;
REPEAT SUM:=-1;
FOR I:=1 TO N DO
FOR J:=1 TO N DO
IF A[I,J]=0 THEN
BEGIN C:=MIN(I,TRUE,FALSE)+MIN(J,FALSE,FALSE);
IF C>SUM THEN
BEGIN SUM:=C;U:=I;V:=J END
END;
M:=A;
A[U,V]:=-5;A[V,U]:=MUCH;
FOR J:=1 TO N DO IF A[U,J]<>-5 THEN A[U,J]:=-1;
FOR I:=1 TO N DO IF A[I,V]<>-5 THEN A[I,V]:=-1;
REDUC;R:=R-1;ZARAD;
A:=M;A[U,V]:=MUCH;REDUC;R:=R+1;ZARAD;
A:=ZACATEK^.MAT;R:=ZACATEK^.ROZMER;G:=ZACATEK^.GAMA;
ZACATEK:=ZACATEK^.NEXT
UNTIL R=2; C:=-1;
FOR I:=1 TO N DO FOR J:=1 TO N DO
IF (A[I,J]=-5)
THEN WRITELN(LST,'hrana ',I,' ',J);
FOR I:=1 TO N DO FOR J:=1 TO N DO
IF A[I,J]=0 THEN BEGIN C:=C+2; POLE[C]:=I;
POLE[C+1]:=J END;
FOR I:=2 TO 4 DO
IF (POLE[2*I-1]<>POLE[1]) AND (POLE[2*I]<>POLE[2]) AND
(POLE[2*I-1]<>0)
THEN BEGIN WRITELN (LST,'hrana ',POLE[1],POLE[2]:2);
WRITELN (LST,'hrana ',POLE[2*I-1],POLE[2*I]:2);
GOTO 9
END;
FOR I:=3 TO 4 DO
IF (POLE[2*I-1]<>POLE[3]) AND (POLE[2*I]<>POLE[4]) AND
(POLE[2*I]<>0)
THEN BEGIN WRITELN (LST,'hrana ',POLE[3],POLE[4]:2);
WRITELN (LST,'hrana ',POLE[2*I-1],POLE[2*I]:2)
END;
9: END.
Vzor struktury vstupních dat.
5
30000 5 7 1 12
4 30000 12 6 30000
1 7 30000 5 15
19 15 17 30000 25
30000 12 24 7 30000
Ošetřená metoda proti uzavření kratších cyklů než jsou Hamiltonovy cykly
v HP-PASCALu
( procedura TEST)
PROGRAM LITTLE(F,LST,input,output);
{ HEWLETT PACKARD HP-PASCAL COMPILER }
{ Pro PC : 1.Zmenit vstup a vystup dat
2.Osetrit velikost HEAPu napr.prubeznym ulozenim na
disk }
CONST MAX=25;MUCH=maxint-1000;
TYPE UKAZ=^ZAZNAM;
MATRIX=ARRAY[1..MAX,1..MAX] OF INTEGER;
ZAZNAM=RECORD
MAT:MATRIX;
GAMA,ROZMER:INTEGER;
NEXT:UKAZ
END;
VAR X,ZACATEK:UKAZ;
A,M:MATRIX;
G,R,U,V,I,J,K,N,SUM,C:INTEGER;
LST,F:TEXT;
log:boolean;pocet,gsum:integer;
FUNCTION TEST:Boolean;
var i,j,uu,vv:integer;t:boolean;
begin uu:=u;vv:=v;t:=true;i:=1;
while t and (i<=n) do
if a[vv,i]=-5 then begin vv:=i;i:=1;
t:= not (uu=vv) end else i:=i+1;
if not t then begin a:=m;a[u,v]:=MUCH end;
Test:=t;
end;
FUNCTION MIN(L:INTEGER;HORZ,SELF:BOOLEAN):INTEGER;
VAR K,MM:INTEGER;t:boolean;
BEGIN MM:=MUCH;t:=true;
CASE HORZ OF
TRUE :FOR K:=1 TO N DO
IF (A[L,K]>=0)
AND (A[L,K]<MM) AND ((L<>I) OR (K<>J) OR SELF)
THEN
begin t:=false;MM:=A[L,K] end;
FALSE:FOR K:=1 TO N DO
IF (A[K,L]>=0)
AND (A[K,L]<MM) AND ((K<>j) OR (L<>i) OR SELF)
THEN
begin t:=false;MM:=A[K,L] end
END;
IF t THEN MIN:=0 ELSE MIN:=MM
END; (* MIN *)
PROCEDURE REDUC;
VAR S,I,J:INTEGER;t:boolean;
BEGIN SUM:=0;t:=false;
FOR I:=1 TO N DO
BEGIN S:=MIN(I,TRUE,TRUE);t:=(s=much) or
t;
IF S>0
THEN FOR J:=1 TO N DO IF A[I,J]>=0 THEN A[I,J]:=A[I,J]-S;
SUM:=SUM+S
END;
FOR J:=1 TO N DO
BEGIN S:=MIN(J,FALSE,TRUE);t:=(s=much) or
t;
IF S>0
THEN FOR I:=1 TO N DO IF A[I,J]>=0 THEN A[I,J]:=A[I,J]-S;
SUM:=SUM+S
END;
if t then sum:=much;
END; (* REDUC *)
PROCEDURE ZARAD;
VAR P,Q:UKAZ;i:integer;
BEGIN P:=ZACATEK;Q:=NIL;i:=1;
if (much>sum)and(much>g) then gsum:=sum+g else gsum:=much;
WHILE (P<>nil)
and((P^.GAMA<GSUM) OR (P^.GAMA=GSUM)
AND (P^.ROZMER<R)) DO
BEGIN Q:=P;P:=P^.NEXT;i:=i+1 END;
if P<>nil then begin
NEW(X);X^.GAMA:=GSUM;X^.MAT:=A;X^.ROZMER:=R;
IF Q=NIL THEN
BEGIN X^.NEXT:=ZACATEK;ZACATEK:=X END
ELSE BEGIN X^.NEXT:=P;Q^.NEXT:=X END;
pocet:=pocet+1
END
END; (* ZARAD *)
procedure ZRUS;
VAR P,Q,X:UKAZ;
BEGIN P:=ZACATEK;WHILE (P^.GAMA<=GSUM) and (p^.rozmer<>0) and
(p^.next<>nil)do
q:=p;p:=p^.next;
WHILE p<>nil do begin x:=p;p:=p^.next;dispose(x) end;
q^.next:=nil;
END;
procedure tiskmat;
var i,j:integer;
begin for i:=1 to n do begin for j:=1 to n do write(lst,a[i,j]:6);writeln(lst)
end
end;
BEGIN REWRITE(LST);
WRITELN(LST,'MATICE VZDALENOSTI');
WRITELN(LST,'------------------');
RESET(F);READLN(F,N);pocet:=0;
FOR I:=1 TO N DO
BEGIN FOR J:=1 TO N DO BEGIN READ(F,A[I,J]);WRITE(LST,A[I,J]:7)
END;
READLN(F);WRITELN(LST)
END;WRITELN(LST);WRITELN(LST);
FOR I:=1 TO N DO A[I,I]:=MUCH;
REDUC;G:=SUM;R:=N;
NEW(ZACATEK);ZACATEK^.NEXT:=NIL;ZACATEK^.GAMA:=MUCH;m:=a;
ZACATEK^.MAT:=a;
REPEAT
REPEAT
SUM:=-1;
FOR I:=1 TO N DO
FOR J:=1 TO N DO
IF A[I,J]=0 THEN
BEGIN C:=MIN(I,TRUE,FALSE)+MIN(J,FALSE,FALSE);
IF C>SUM THEN
BEGIN SUM:=C;U:=I;V:=J END
END;
if r>1 then begin
log:=test;
if not log then begin
reduc;
zarad;
a:=zacatek^.mat;r:=zacatek^.rozmer;
g:=zacatek^.gama;
x:=zacatek;zacatek:=zacatek^.next;dispose(x);pocet:=pocet-1;
end; end
else log:=true;
UNTIL log;
M:=A;
if (R>1)and(a[v,u]>=0) then A[v,u]:=MUCH;a[u,v]:=-5;
FOR J:=1 TO N DO IF A[U,J]<>-5 THEN A[U,J]:=-1;
FOR I:=1 TO N DO IF A[I,V]<>-5 THEN A[I,V]:=-1;
writeln('Pocet konc.matic:',pocet:10);
REDUC;R:=R-1;ZARAD;if r=0 then ZRUS;
A:=M;A[U,V]:=MUCH;REDUC;R:=R+1;ZARAD;
A:=ZACATEK^.MAT;R:=ZACATEK^.ROZMER;G:=ZACATEK^.GAMA;
x:=zacatek;ZACATEK:=ZACATEK^.NEXT;dispose(x);pocet:=pocet-1;
m:=a;
UNTIL R=0;
WRITELN(LST,'OPTIMALNI CESTA OBCHODNIHO CESTUJICIHO');
WRITELN(LST,'======================================');
WRITELN(LST,'DELKA CESTY:',G);WRITELN(LST,'VYPIS
HRAN CESTY:');
FOR I:=1 TO N DO FOR J:=1 TO N DO
IF (A[I,J]=-5)
THEN WRITELN(LST,'hrana ',I,' ',J);
WRITELN(LST,'VYPIS VRCHOLU CESTY');
I:=1;J:=1;WRITE(LST,I:2);WHILE J<=N DO begin
K:=1;
WHILE (J<=N) AND (K<=N) DO
IF A[I,K]=-5 THEN BEGIN J:=J+1;I:=K;WRITE(LST,'-',K:2);k:=k+1
END else k:=k+1 end;
WRITELN('HOTOVO!!!');close(lst);close(f)
END.
Místo znaků zde používáme dostatečně velká čísla typu integer. Jiné
metody řešení tohoto problému je možné najít v příloze 11.5
Metoda elastické neuronové sítě a 11.6 Corn -fleks
metoda
3.5 Minimální pokrytí grafu a optimální cesty v grafech.
Předpokládejme, že je nyní naším cílem spojit určitá místa telefonní či
železniční sítí tak, aby její délka byla minimální. Je zřejmé, že tuto
síť můžeme zobrazit jako hranově ohodnocený graf.Minimální spojení mezi
všemi požadovanými místy bude realizovat souvislý graf s minimálním počtem
hran - tedy strom. Naším úkolem je najít mezi všemi pokrývajícími stromy
ten, který bude mít minimální součet délek všech stran. Uveďme si jednoduchý
algoritmus výběru minimálního pokrývajícího stromu grafu:
KROK 1. Položíme počet vybraných hran i=1. Vybereme hranu s minimálním
ohodnocením.
KROK 2. Položíme i=i+1 a pokud je i<n-1 (počet vrcholů grafu), pak vybereme
další hranu s minimální délkou ze zbývajících (ještě nevybraných) hran
grafu a to takovou, která s předchozími nevytvoří cyklus.
KROK 3. Krok 2 opakujeme do té doby, dokud je to možné.
Příklad.
Nalezněte minimální pokrývající strom grafu, který je zobrazen na následujícím
obrázku.
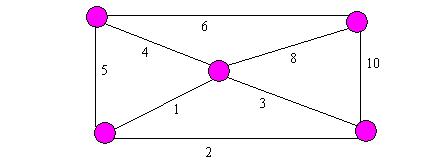
Obr.14
Postup výběru minimálního stromu v tomto příkladu je následující:
(4,5),(3,4),(1,5),(1,2)
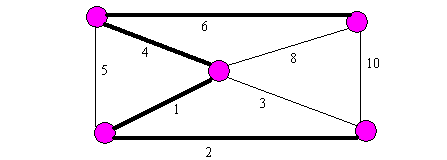
Obr.15
Program pro nalezení minimálního pokrývajícího stromu.
PROGRAM MPG;
VAR I,J,M,N,N1,N2,K,W:INTEGER;
L:0..1;
LA,ID:ARRAY[1..20] OF 0..1;
NB,NE,VAL:ARRAY[1..20] OF INTEGER;
BEGIN
WRITE('ZADEJ POCET HRAN A UZLU:');READLN(M,N);
{M-POCET HRAN,N-POCET VRCHOLU}
FOR I:=1 TO M DO BEGIN READ(NB[I],NE[I],VAL[I]);ID[I]:=0 END;
{GRAF ZADAME POMOCI HRAN - PRVNI JE CISLO UZLU ZACATEK HRANY,
NASLEDUJE CISLO UZLU-KONEC HRANY A TRETI CISLO JE DELKA HRANY}
LA[1]:=1;
FOR J:=2 TO N DO LA[J]:=0;K:=0;
WHILE K<N-1 DO BEGIN
L:=0;FOR I:=1 TO M DO BEGIN IF ID[I]<>1 THEN BEGIN
N1:=NB[I];N2:=NE[I];
IF LA[N1]+LA[N2]=1 THEN IF L=0 THEN BEGIN
L:=1;W:=VAL[I];J:=I END
ELSE
IF VAL[I]<W THEN BEGIN W:=VAL[I];
J:=I END
END
END;
ID[J]:=1;N1:=NB[J];N2:=NE[J];
IF LA[N1]=0 THEN LA[N1]:=1;LA[N2]:=1;K:=K+1
END;
WRITELN('VÝSLEDKY: - MINIMÁLNI POKRYTÍ GRAFU');
WRITELN('POČÁTEK KONEC DÉLKA HRANY');
FOR I:=1 TO M DO IF ID[I]=1 THEN WRITELN(NB[I]:10,NE[I]:10,VAL[I]:10);
END.
Příklad vstupních dat. Příklad výstupní sestavy.
| 10 7
|
VÝSLEDKY: - MINIMÁLNÍ POKRYTÍ GRAFU
|
| 1 2 3
|
POČÁTEK KONEC DÉLKA HRANY
|
| 1 3 7
|
1 2 3
|
| 2 4 5
|
2 4 5
|
| 3 4 2
|
3 4 2
|
| 3 5 6
|
4 6 2
|
| 2 6 6
|
4 5 1
|
| 4 6 2
|
5 7 3
|
| 4 5 1
|
|
| 6 7 7
|
|
| 5 7 3
|
|
Výpočet minimální kostry grafu v JavaScriptu
Algoritmy výběru nejkratších nebo nejdelších cest mezi dvěma vrcholy souvislého
grafu nacházejí aplikace v nejrůznějších oblastech činnosti a my se s nimi
ještě v dalším textu setkáme. Význam těchto úloh je pro nás intuitivně
spojen s nalezením nejkratších vzdáleností v grafu a s problémy minimalizace
především přepravních nákladů. Pojem nejdelší cesty pak figuruje především
v úlohách určení kritické cesty v síťovém grafu a optimalizačních úlohách
na síťových grafech. Bezprostřední vliv těchto algoritmů se projevil v
zásadní změně metod řešení úloh trasování v dopravě.
Předpokládejme, že máme k dispozici část silniční mapy, kterou můžeme popsat
jako neorientovaný graf, ve kterém křižovatky tvoří vrcholy grafu a spojnice
křižovatek hrany. Ohodnocení grafu jsou vzdálenosti mezi křižovatkami.
Úkolem je najít nejkratší cestu, která spojuje dvě zadané křižovatky v
mapě.
Algoritmus Forda-Fulkersona.
Pro řešení naší úlohy zavedeme nové proměnné, které označíme jako wi,
a které přiřadíme každému vrcholu grafu. Jejich faktický význam bude vzdálenost
od prvního zadaného vrcholu do daného vrcholu i.
Nechť počátečním vrcholem hledané cesty je vrchol s číslem 1.
KROK 1. Položme w1=0 a wi= pro každé i:i#1.
KROK 2. Nalezneme hrany uij pro jejichž ohodnocení dij
platí následující vztah
(3.1) wj - wi > dij,
pro takto nalezenou hranu (i,j) ,pokud existuje ,změníme ohodnocení vrcholu
wj podle následujícího pravidla
wj = wi + dij
KROK 3. Vrátíme se zpět ke kroku 2 a tento postup opakujeme do té doby,
dokud existují hrany,pro které je splněn vztah 3.1. Nechť koncovým vrcholem
cesty je vrchol q, pak wq udává délku nejkratší cesty mezi
vrcholem 1 a vrcholem q.
Zbylým problémem je najít posloupnost hran, která tuto cestu realizuje.
Posloupnost hran určujeme zpětně od vrcholu q grafu. Podle postupu
určení hodnot wj je zřejmé, že se musí najít minimálně jeden vrchol
j takový, že
wq - wj = dqj
a analogicky můžeme postupovat tímto způsobem dále, až dosáhneme výchozí
vrchol grafu.
Mohou nastat i situace, které jsme zatím nepředvídali. Jednou z nich je
ta, kdy není možné aplikovat krok 2 algoritmu a wq= . V takovém
případě je graf nesouvislý a cesta mezi vrcholy 1 a q neexistuje.
Podstatně lepší je úprava algoritmu, kterou provedl Dantzig. Odstranil
chaotičnost výpočtu a dosáhl toho, že každý vrchol grafu získá ohodnocení
wj pouze jednou a to následujícím způsobem
(3.2) wk = m i n {wi + dij}
V tomto vztahu se minimum počítá pro všechna i ,pro která je již
definována hodnota wi a pro všechna j, pro která wj
dosud definována není a přitom existuje hrana uij. Celý výpočet
je možné organizovat jak v samotném grafu, tak i v tabulce. V případě malého
grafu je výhodnější výpočet provádět v grafu. V případě složitějšího grafu
je lepší používat tabulku.
Příklad.
Nechť je zadán graf pomocí jednotlivých hran a jejich délek.
| Počáteční vrchol
|
Koncový vrchol
|
délka hrany
|
| 1
|
2
|
16
|
| 1
|
4
|
12
|
| 1
|
5
|
7
|
| 1
|
6
|
19
|
| 1
|
7
|
11
|
| 2
|
3
|
9
|
| 2
|
4
|
18
|
| 2
|
7
|
17
|
| 2
|
8
|
11
|
| 2
|
9
|
24
|
| 3
|
4
|
28
|
| 3
|
9
|
12
|
| 4
|
5
|
14
|
| 5
|
6
|
10
|
| 6
|
7
|
18
|
| 7
|
8
|
21
|
| 8
|
9
|
16
|
Nyní sestavíme tabulku, ve které v prvním řádku budeme uvádět hodnotu wi
, v druhém řádku číslo uzlu a v dalších řádcích jednotlivé uzly, které
jsou z daného přímo dosažitelné. Řekněme, že naším cílem je najít nejkratší
cestu z vrcholu 6 do vrcholu 9.
| wi
|
|
|
|
|
|
0
|
|
|
|
| i
|
==1=
|
==2=
|
==3=
|
==4=
|
==5=
|
==6=
|
==7=
|
==8=
|
==9=
|
|
|
|
|
|
|
|
1(19)
|
|
|
|
|
|
|
|
|
|
|
5(10)
|
|
|
|
|
|
|
|
|
|
|
7(18)
|
|
|
|
Nyní vypočteme minimum pro ještě neoznačené sloupce, k tomu můžeme využít
zatím pouze sloupce 6. Provádíme to tak, že sčítáme odpovídající
hodnotu wi s hodnotou uvedenou v závorce,t.j. 0+19, 0+10, 0+18.
Minimální hodnota je deset a dosahuje se ve vrcholu pět, označíme tedy
tento vrchol hodnotou w5=10 a vypíšeme všechny dosažitelné hrany
s jejich délkou.
| wi
|
|
|
|
|
10
|
0
|
|
|
|
| i
|
==1=
|
==2=
|
==3=
|
==4=
|
==5=
|
==6=
|
==7=
|
==8=
|
==9=
|
|
|
|
|
|
|
1(7)
|
1(19)
|
|
|
|
|
|
|
|
|
|
4(14)
|
5(10)
|
|
|
|
|
|
|
|
|
|
6(10)
|
7(18)
|
|
|
|
Nyní dostáváme hodnoty součtů 10+7, 10+14, 10+10, 0+19, 0+18, minimum je
v tomto případě sedmnáct a dosahuje se na vrcholu 1.
| wi
|
17
|
|
|
|
10
|
0
|
|
|
|
| i
|
==1=
|
==2=
|
==3=
|
==4=
|
==5=
|
==6=
|
==7=
|
==8=
|
==9=
|
|
|
2(16)
|
|
|
|
1(7)
|
1(19)
|
|
|
|
|
|
4(12)
|
|
|
|
4(14)
|
5(10)
|
|
|
|
|
|
7(11)
|
|
|
|
6(10)
|
7(18)
|
|
|
|
Další kroky přeskočíme a uvedeme hned již závěrečnou tabulku, ve které
čísla sloupců vznikala postupně, podle velikosti a ve sloupcích jsou uváděny
pouze vrcholy, které ještě nemají ohodnocení.
| wi
|
17
|
33
|
42
|
24
|
10
|
0
|
18
|
39
|
54
|
| i
|
==1=
|
==2=
|
==3=
|
==4=
|
==5=
|
==6=
|
==7=
|
==8=
|
==9=
|
|
|
2(16)
|
3(9)
|
9(12)
|
2(18)
|
1(7)
|
1(19)
|
2(17)
|
9(16)
|
|
|
|
4(12)
|
9(24)
|
|
3(28)
|
4(14)
|
5(10)
|
8(21)
|
|
|
|
|
7(11)
|
|
|
|
6(10)
|
7(18)
|
|
|
|
Zjistili jsme, že délka minimální cesty je 54 jednotek a je třeba ještě
určit, kudy vede. Začneme od konce a zjistíme, ze kterého sloupce jsme
dosáhli hodnotu 54. Ve všech sloupcích nalezneme hodnoty 9 a sečteme hodnotu
wi s hodnotou uvedenou v závorce. Pokud tato hodnota dá 54, pak
jsme se dostali do vrcholu 9 z tohoto sloupce a tento sloupec můžeme
považovat za konec cesty a zopakovat všechny předchozí kroky. Tento postup
ilustrují v následující tabulce pole, označená čtverečkem.
wi 17 33 42 24 10 0 18 39 54
i 1 2 3 4 5 6 7 8 9
2(16) 3(9) 9(12) 2(18) 1(7) 1(19) 2(17) 9(16)
4(12) 9(24) 3(28) 4(14) 5(10) 8(21)
7(11) 6(10) 7(18)
Vidíme tedy, že optimální cesta vede přes vrcholy 6-5-1-2-3-9.
Analogický algoritmus pro orientovaný graf předvádí metoda uvedená v příloze
11.7 algoritmus Dijkstra
V některých případech je třeba znát nejen nejmenší vzdálenost mezi určitou
dvojicí vrcholů, ale mezi libovolnou dvojicí vrcholů v grafu. Použití výše
uvedeného algoritmu je v tomto případě značně neefektivní. Pro řešení uvedené
úlohy je možné využít operace minimálního sčítání.
Definujme operaci minimálního sčítání následujícím způsobem pro matice
A. B typů (p,q) a (q,r):
C = A (+) B ,kde cij= m i n {aik +akj}
1<k<q
Pro výpočet všech nejkratších vzdáleností v grafu je třeba mít k dispozici
matici vzdáleností grafu, kterou pak považujeme za výchozí matici. Označme
si ji např. D0. Při vypočtu pak postupujeme tak, že použijeme operaci
minimálního sčítání k vytvoření matice D1 podle následujícího vztahu
D1 = D0 (+) D0
Matice D1 obsahuje všechny minimální vzdálenosti, které jsou tvořeny
cestami z jedné nebo dvou hran. Analogicky můžeme z matice D1 vytvořit
matici D2 atd. Protože nevíme, jak dlouhá nejkratší cesta bude,(
co se týká počtu hran) musíme v tomto postupu pokračovat tak dlouho, až
bude platit, že Di+1 = Di.
Program pro nalezení minimálních vzdáleností v grafu.
PROGRAM MIRA;
(* URČENÍ MINIMÁLNÍCH VZDÁLENOSTÍ V GRAFU*)
TYPE JMENO=ARRAY[1..10] OF CHAR;
VAR I,J,K,L,JJ,I1,I2,P:0..100;
A:CHAR;M,II,S,N:INTEGER;LOG:BOOLEAN;
Q:ARRAY[1..100] OF JMENO;
B:JMENO;
D:ARRAY[1..100] OF INTEGER;
FUNCTION WW(I,J:INTEGER):INTEGER;
BEGIN WW:=(I-1)*(M-(I-2) DIV 2)+J-I+1 END;
BEGIN
WRITE('ZADEJ POČET VZDÁLENOSTÍ');READ(M);L:=0;
FOR I:=1 TO M DO FOR J:=1 TO M DO
IF I=J THEN D[WW(I,J)]:=0 ELSE D[WW(I,J)]:=32500;
FOR II:=1 TO M DO BEGIN
FOR JJ:=1 TO 2 DO BEGIN A:=CHR(13);WHILE A<'A' DO READ(A);J:=1;
WHILE (A>='A')AND(A<='Z')AND(A<>' ') DO BEGIN B[J]:=A;
READ(A);J:=J+1 END;
FOR I:=J TO 10 DO B[I]:=' ';K:=0;
FOR I:=1 TO L DO IF Q[I]=B THEN K:=I;
IF K=0 THEN BEGIN L:=L+1;Q[L]:=B;K:=L END;
IF JJ=1 THEN I1:=K ELSE I2:=K END;
IF I2<I1 THEN BEGIN P:=I1;I1:=I2;I2:=P END;READLN(N);
I1:=WW(I1,I2);D[I1]:=N END;
LOG:=TRUE;
WHILE LOG DO BEGIN LOG:=FALSE;
FOR I:=1 TO M DO
FOR J:=I+1 TO M DO BEGIN S:=D[WW(I,J)];
FOR K:=1 TO M DO BEGIN
IF K IN [I..J] THEN BEGIN I1:=WW(I,K);I2:=WW(K,J) END;
IF K<I THEN BEGIN I1:=WW(K,I);I2:=WW(K,J) END;
IF K>J THEN BEGIN I1:=WW(I,K);I2:=WW(J,K) END;
IF S>D[I1]+D[I2] THEN BEGIN S:=D[I1]+D[I2];
LOG:=TRUE END END;
D[WW(I,J)]:=S END END;
FOR I:=1 TO L DO BEGIN WRITE(Q[I]);
FOR I1:=1 TO L DO IF I1<I THEN WRITE(' ') ELSE WRITE(D[WW(I,I1)]:4);
WRITELN END
END.
Příklad vstupních dat. Příklad výstupní sestavy.
4
blansko adamov 9 blansko 0 9 12 15
blansko sloup 12 adamov 0 21 4
blansko krtiny 15 sloup 0 27
adamov krtiny 4 krtiny 0
3.6 Sítě, optimalizační úlohy na sítích.
Definice 3.16
Sítí nazýváme takový souvislý graf, ve kterém jsou vyčleněny některé podmnožiny
vrcholů grafu ( obvykle dvě), nazývané póly sítě (stup a výstup).
POZNÁMKA. V dalším textu budeme používat pouze orientovaný, souvislý,
hranově ohodnocený graf se dvěma póly. Budeme předpokládat, že ohodnocení
hran jsou nezáporná čísla. Tato čísla budeme nazývat propustností a prakticky
je považovat za hodnotu, která z nějakých důvodů nesmí být překročena.
Z praktického hlediska může být tímto způsobem znázorněna síť vodovodní,
silniční, plynová apod.
Definice 3.17
Proudem, tokem v síti, nazýváme dvojici (f,w), kde w je určitá
orientace sítě a f(u) je nezáporná funkce,zadaná na množině všech
hran. Hodnoty této funkce nepřevyšují propustnosti hran a v každém vnitřním
uzlu vyhovují následující podmínce:
0< f(u) < b(u) omezení propustnosti
R(a) = E f(u) - E f(u) = 0
uEG(a) uEH(a)
kde G(a) je množina všech hran, které vstupují do vrcholu a sitě
a H(a) je množina všech hran, které z vrcholu a vystupují. Dále
můžeme zavést hodnotu ceny jednotky přepravované po hraně u sítě
c(u).
Při těchto omezeních a označeních můžeme nyní zformulovat několik extremálních
problémů na sítích:
1.Minimalizujte sumární cenu zadaného proudu v síti.
2.Nalezněte maximální možný proud v síti.
Definice 3.18
Nenasycenou (augmentální) cestou nazveme takovou cestu v síti, která vede
ze vstupu do výstupu a jejíž každá hrana má kladnou propustnost.
V dalším textu se budeme zabývat pouze algoritmem nalezení maximálního
proudu v síti. Proudy po hranách u nebudeme používat přímo, ale
prostřednictvím změn ohodnocení propustností jednotlivých hran a opačně
orientovaných hran. Budeme předpokládat, že zadané propustnosti jsou konstantní
bu. Symbol du budeme používat pak pro změněnou propustnost hrany.
Nechť je zadána hrana e=(i,j)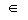 EU.
Rozšíříme množinu U tak, že do ní zařadíme i hranu g=(j,i).
Budeme dále předpokládat, že de=be-xe a dg=xe
, kde xe je určitá hodnota proudu v některé iteraci algoritmu.
EU.
Rozšíříme množinu U tak, že do ní zařadíme i hranu g=(j,i).
Budeme dále předpokládat, že de=be-xe a dg=xe
, kde xe je určitá hodnota proudu v některé iteraci algoritmu.
Růst proudu podél určité nenasycené cesty probíhá díky poklesu změněných
propustností každé hrany o hodnotu o. Největší hodnota o, která nenarušuje
žádné z omezení je rovna minimální propustnosti podél této nenasycené cesty.
Algoritmus výpočtu probíhá po přípustných proudech (jedná se tedy o přímý
algoritmus výpočtu). Proudu přiřadíme nejprve nulovou hodnotu, takové řešení
je přípustné, ale pravděpodobně nikoliv optimální. Další částí je nalezení
nenasycené cesty a zvýšení proudu jejím prostřednictvím. Pro nalezení této
cesty můžeme využít algoritmu, který bude analogický algoritmu Forda-Fulkersona,
s kterým jsme se již seznámili v předchozích paragrafech.
KROK 0. Nechť všechny vstupy jsou označeny, ale nejsou prohlédnuty a všechny
ostatní uzly jsou neoznačeny.
KROK 1. Vybereme libovolný označený, ale neprohlédnutý uzel i.
KROK 2. Prohlédneme všechny hrany e(i,j) s propustností de>0,
které spojují uzel i s ještě neoznačenými uzly j. Označíme
uzly j a hrany ej=(i,j). Nyní můžeme považovat vrchol i
za označený a prohlédnutý a uzel j označen a neprohlédnut. Jestliže
je výstup ze sítě označen je nenasycená cesta nalezena, v opačném případě
přecházíme ke kroku 3.
KROK 3. Nechť uzel i je označen a prohlédnut. Přecházíme ke kroku 1 a postup
opakujeme do té doby, dokud existují označené a neprohlédnuté uzly.
Jestliže je algoritmus ukončen krokem 2 je nenasycená cesta nalezena,je-li
ukončen krokem 3, pak již nenasycená cesta v síti neexistuje.
Věta 3.6.1
Výše uvedený algoritmus nalezení maximálního proudu v síti je konečný.
Důkaz.
Je zřejmé, že v případě celých hodnot propustností se proud v síti při
každém kroku zvýší minimálně o jednu jednotku a i změněná propustnost zůstane
celočíselnou. Dále je zřejmé, že výše uvedený algoritmus dovede najít vždy
nenasycenou cestu, pokud tato cesta existuje. Bohužel není již tak jednoduché
dokázat, že v případě, kdy neexistuje nenasycená cesta je získaný proud
v síti maximální.
Definice 3.19
Řez sítě nazýváme prostým řezem, pokud tento řez po vynechání jakékoliv
jedné hrany již přestává být řezem. Propustností tohoto řezu D(w) nazveme
součet propustností jednotlivých hran, které tento řez obsahuje.
Věta 3.6.2 (Forda-Fulkersona)
Maximální proud v síti je roven minimální propustnosti prostého řezu sítě.
Důkaz.
Označme maximální proud jako Qmax a minimální řez jako Dmin.
Nejprve dokažme, že Qmax<Dmin. Abychom dokázali tento
fakt, stačí dokázat,že pro libovolný řez a libovolný proud v síti platí
Q < D, a to je zřejmé z fyzického smyslu úlohy. Sečteme hodnoty
R(a) po všech vrcholech 'a' sítě, z jedné strany je to hodnota rovná Q
a z druhé strany je to algebraický součet hodnot všech proudů jdoucích
řezem zleva doprava. Jelikož f(u)<d(u) získáme potřebnou nerovnost.
Dokažme nyní,že v síti lze vytvořit proud rovný Dmin. Důkaz provedeme
indukcí podle počtu hran sítě. Nechť je počet hran nulový, to znamená,
že síť je složena z izolovaných vrcholů. Je zřejmé, že v takovém případě
Q = Dmin = 0. P5edpokl8dejme nyní, že pro libovolnou síť,
obsahující p hran je věta již dokázána. Dokažme nejprve následující
větu:
Věta 3.6.3
V síti je možné vytvořit libovolný proud, který je menší než Dmin.
Důkaz.
Nalezneme v síti řez s propustností Dmin. Snížíme tuto propustnost
na hodnotu Q a podle předpokladu indukce v dané síti musí existovat daný
proud. Je zřejmé, že tento proud musí existovat i v původní síti. Věta
je dokázána.
Využijeme-li dokázanou větu pro důkaz věty Forda-fulkersona a snížíme některé
propustnosti tak, aby byly splněny následující podmínky:
1. Propustnost každého prostího řezu není menší než Dmin.
2. Každá hrana je správně orientovaná (zleva doprava) v některém minimálním
řezu nebo má nulovou propustnost.
Jestliže v takto zvolené síti existují hrany s nulovou propustností, pak
je můžeme odstranit a vznikne síť s méně než p hranami a ta splňuje
větu podle předpokladu indukce. Zbylé případy můžeme rozdělit na dvě kategorie:
A. Každá cesta obsahuje ne víc než dvě hrany.
B. Existuje cesta, která obsahuje alespoň tři hrany.
V případě A se jedná o paralelní spojení určitého počtu hran spojujících
přímo vstup a výstup sítě a určitých podsítí. Situace je znázorněna na
následujícím obrázku č.14
Obr.16
Je jasné,že prostými řezy mohou být pouze takové množiny hran, které obsahují
přímé spojení vstupu a výstupu a v každé podsíti jsou orientovány buď zleva
doprava nebo naopak. Odtud plyne, že součet propustností v levé části musí
být stejný jako součet propustností v pravé části, ale v takovém případě
lze vzít proud rovný přímo propustnosti dané hrany a věta je dokázána.
V případě B obsahuje síť vnitřní hranu. Vezměme minimální řez, který obsahuje
tuto hranu a každou hranu tohoto řezu nahraďme seriovým spojením dvou hran
se stejnou propustností. Sjednocením vrcholů, dělících tyto hrany vznikne
seriové spojení dvou sítí. Každá z těchto sítí opsahuje méně než p hran
a věta je dokázána zcela a úplně.
3.7 Matematické základy metod síťové analýzy.
Definice 3.20
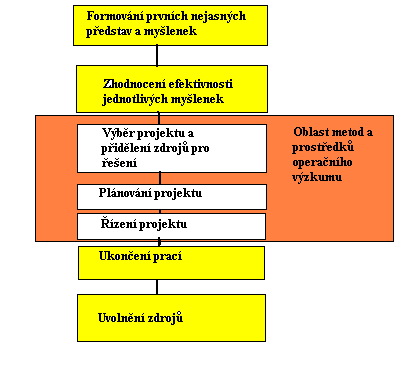
Projektem nazýváme komplex vzájemně spojených prací, k jejichž vykonání
jsou vyčleněny určité prostředky a jsou stanoveny určité doby pro jejich
vykonání.
Projektem v širokém slova smyslu chápeme cestu od mlhavé, nejasné myšlenky
ke konečnému produktu, výrobku, stavbě apod. Etapy zpracování projektu
jsou znázorněny na následujícím obrázku č.16. Dále se budeme zabývat jen
některými částmi této složité činnosti a to těmi, ve kterých mohou být
použity optimalizační metody operačního výzkumu.
3.8 Metody a modely výběru projektu.
Modely výběru projektu by měly sloužit vedoucím pracovníkům ke stanovení
priorit mezi jednotlivými projekty a k jejich posouzení z nejrůznějších
hledisek. Umožňují z mnoha alternativ vyčlenit prostředky a zdroje na to,
co je optimální a efektivní a to později realizovat. Existují tři základní
typy modelů tohoto procesu, založené na hodnoceních expertů, na ekonomických
ukazatelích a na rozdělování objemu kapitálových investic.
První dva typy byly založeny a vypracovány a jsou využívány především vedoucími
pracovníky, praktiky pro řešení otázky výhodnosti a priorit jednotlivých
projektů. Poslední skupina metod - rozdělování kapitálových investic se
využívá především pro optimální rozdělování prostředků, které jsou k dispozici.
3.8.1. Expertní hodnocení.
Jestliže projekty mají spíše výzkumný charakter, pak obyčejně nemáme k
dispozici dostatečně kvalitní objektivní informace o projektech, nákladech,
realizovatelnosti a následně všechny řídící proměnné v optimalizačních
modelech bývají vysoce neurčité. Především v těchto případech se využívají
názory dostatečně zkušených a odborně zdatných jednotlivců, odborníků v
dané oblasti, kterým říkáme experti.
Jejich pozice pro použití určité soustavy kritérií a charakteristik projektu,
kterým by měl vyhovovat projekt vyhovovat, bývají obvykle přínosem pro
optimální rozhodování.
Velmi často je využíván bodovací systém. V tomto systému bývá určitým počtem
bodů ohodnocen každý z navrhovaných projektů a každému z expertů je přiřazena
určitá váha (podle jeho postavení, praxe, zkušeností apod.) .Pokud má bodovací
systém vícekriterií, jsou váhy přiřazeny i jednotlivým kriteriím. Hodnocení
projektu má pak charakter ekonomické konvoluce jednotlivých kritérií a
jednotlivých expertů.
Uveďme si příklad hodnocení jednoho projektu jedním expertem.
Bodovací systém je 1 až 10 bodů pro každé ze tří uvedených kriterií.
| Kriterium
|
Váha
|
Hodnocení
|
celkem
|
| Pravděpodobnost realizace
|
3
|
5
|
15
|
| Zisk z realizace
|
2
|
10
|
20
|
| Náklady
|
1
|
3
|
3
|
| Celkové hodnocení
|
|
|
38
|
Úspěšnost projektu je možné výjádřit i v procentech: 38/60*100==63.333
% , 60 je maximální možný dosažitelný počet bodů při hodnocení.
Může vznikat i otázka rozdělení projektů do několika skupin, na základě
kterých lze vybrat určit určité měřítko hodnocení.
Příklad.
Předpokládejme, že v posledních dvou letech kolísala cena projektů v rozmezí
od 5 do 15 miliónů Kčs a distribuční funkce nákladů pro 21 realizovaných
projektů odpovídala následující tabulce:
| 5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
| *
|
|
*
|
*
|
*
|
*
|
**
|
**
|
*
|
*
|
*
|
|
|
|
|
|
|
|
**
|
**
|
|
*
|
|
|
|
|
|
|
|
|
*
|
*
|
|
|
|
|
|
|
|
|
|
|
*
|
|
|
|
|
| 1
|
1
|
1
|
1
|
1
|
1
|
2
|
2
|
2
|
3
|
3
|
Podle takto zvoleného měřítka je možné rozdělit projekty do tří skupin
a ohodnotit je odpovídajícím způsobem jedním, dvěma nebo třemi body. V
uvedeném příkladě jsme použili čistě stochastický přístup. Tímto způsobem
se dá i pro kvalitativní kritéria použít kvantitativního hodnocení. Je
možné využít i kombinace hodnocení kvantitativních a kvalitativních.
3.8.2. Ekonomické ukazatele.
Stanovení priority možných variant projektů v období hodnocení projektu
a rozdělení zdrojů se provádí na základě různých ekonomických ukazatelů:
Ukazatel Ansoffa:
Ukazatel kvality projektu = (r*d*p*(T+B)*E*)/(Sk)
Popis jednotlivých označení je následující:
r pravděpodobnost úspěšného ukončení prací
d pravděpodobnost úspěšného zavedení do praxe
p pravděpodobnost úspěšné realizace
T technický ukazatel projektu
B ekonomický ukazatel projektu
E* relativní důchod,který projekt přinese
Sk celkové kapitálové investice
Dalším z celé plejády používaných ukazatelů je
Ukazatel Olsena:
význam projektu = (r*d*p*s*p*n)/(cena projektu)
s roční prodej produkce
p důchod, který realizuje prodej jednotky produkce
n doba trvání projektu
(ostatní položky jsou stejné jako u ukazatele Ansoffa)
Ukazatel Harta:
návratnost kapitálu = (p*G*)/(R*+ D*+ F*+
W)
X* označuje vždy relativní hodnotu uvedené veličiny
G hrubý zisk
R náklady na výzkum
D náklady na zavedení do praxe
F přímá spotřeba základních fondů
W provozní kapitál
Ukazatelů těchto typů se používá poměrně běžně v průmyslové i stavební
praxi. Mimo tyto ukazatele existuje i řada dalších: Villderse, Dismana
apod.
3.8.3. Metody a modely rozdělení kapitálových investic.
V modelech rozdělování kapitálových investic je stanovena implicitně priorita
možných variant v souladu s rozměry vyčleněných prostředků. V obecném případě
může být vytvořen matematický model úlohy následujícího typu:
max 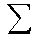 vj(xj)
přitom
vj(xj)
přitom 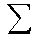 xj <
B.
xj <
B.
B je celkové množství prostředků, které jsou k dispozici, xj
jsou prostředky, které budou vyčleněny na j-tý projekt. Jednotlivé
funkce mohou mít nejrůznější povahu, mohou být nelineární, lineární, konstantní
pro daný projekt. V posledním případě, při konstantních hodnotách pro každý
z projektů se model stává modelem ekonomických ukazatelů. vj je
přitom ukazatelem priority jednotlivých projektů.
3.9 Matematické metody síťového (kalendářního) plánování.
Pokud je již přijato rozhodnutí o započetí prací nad vybraným projektem,
je obyčejně třeba vyřešit úlohu o dokončení projektu (sestavit harmonogram
provádění jednotlivých prací) za zadaný čas a s vyčleněnými prostředky.
Pro řešení této úlohy byly v letech 1956-1958 vypracovány dvě metody. Jednou
z nich je metoda kritické cesty (Critical Path Method - zkráceně
CPM), která byla poprvé použita společností DuPont Co. a
byla dále rozvinuta v pracích firmy Mauchly Associates. Druhou je
metoda ocenění a přehodnocení projektu , známá pod názvem PERT (
Project Evaluation and Review Technique), která byla vypracována
pro ministerstvo válečného námořnictva USA v souladu s programem výroby
ponorek, vybavených raketami Polaris.
Charakteristickým rysem těchto metod je zobrazení projektu ve tvaru grafu,
přesněji řečeno v souvislosti s body zahájení a ukončení realizace projektu
ve tvaru sítě. Síť zobrazuje kauzální (příčinné) vztahy mezi jednotlivými
činnostmi - tedy vpodstatě topologickou návaznost jednotlivých prací na
sebe. Například nejprve musí být proveden výkop, potom betonáž základů
a teprve pak je možné postavit zeď z cihel, ne naopak.
3.9.1. Zobrazení projektu ve tvaru sítě.
Síťové plánování začínáme sestavením seznamu prováděných činností (prací),
ohodnocením jejich délky trvání a určením topologických návazností na sebe.
K tomu účelu je možné využít podkladů nejrůznějšího typu, například normy
apod. Práce zobrazíme jako orientované hrany sítě, orientace těchto hran
pak ukazuje průběh jednotlivých činností projektu (viz obr.17)
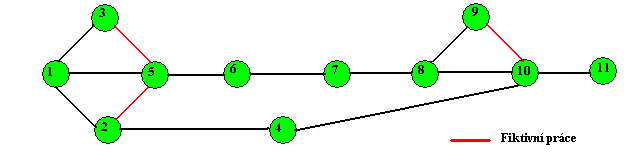
Obr.17
Události,které odpovídají počátkům a koncům jednotlivých činností jsou
zobrazeny jako uzly sítě. Abychom nemuseli popisovat jednotlivé hrany šipkami,
je možné se dohodnout tak, že počáteční vrchol činnosti budeme označovat
uzlem s nižším číslem než vrchol koncový.
Existují určitá pravidla, která musíme respektovat při sestavení sítě:
1. Žádné dvě práce nemohou být identifikovány se dvěma stejnými událostmi.
To znamená, že následující část sítě nesprávně zobrazuje stejné ukončení
dvou prací.
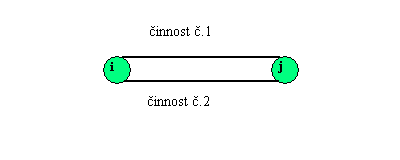
Obr.18
Takovou situaci musíme zobrazit tak, jak ukazuje následující obrázek. Čárkovaně
označujeme tzv. fiktivní práce. Jsou to práce, které reálně neexistují,
mají nulovou dobu trvání a nulové nároky na zdroje. Slouží pouze k zachycení
správné topologie sítě.
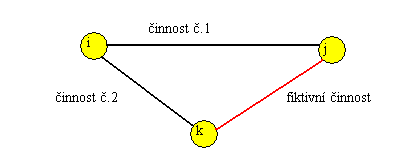
Obr.19
2. Vztahy předcházení a následování musí být zachovány v celé síti. Předpokládejme,
že činnost 5 následuje za činnostmi 2 a 4, které následují za činností
3. V takovém případě část sítě, která zobrazuje tuto situaci, vypadá následovně
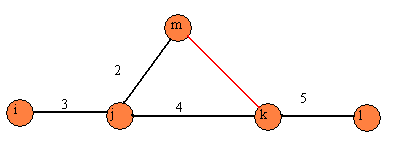
Obr.20
To vše ovšem pouze v případě, že požadujeme, aby práce 5 byla zahájena
až po ukončení práce 2. Pokud tento požadavek nemáme, pak bude výše uvedená
část sítě vypadat následujícím způsobem:
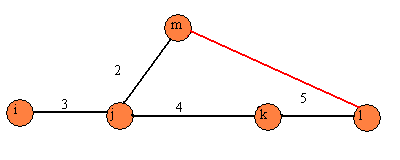
Obr.21
Realizace obou těchto pravidel je znázorněna také na úvodním obrázku č.17.
Činnosti jako takové obyčejně popisujeme analyticky pomocí počátečních
a koncových uzlů, pomocí délek činností a případně i nároků na jiné zdroje
než časové.
3.9.2. Kritická cesta v síťovém grafu.
Definice 3.21.
Kritickými nazýváme ty činnosti v síťovém grafu, jejichž prodloužení povede
k ekvivalentnímu zdržení dokončení celého projektu. Cesta v síti, která
je sestavena z kritických činností, se nazývá kritickou cestou. Délku kritické
cesty budeme nazývat kritickou dobou.
Poznámka.
V definici kritické cesty z ČSN 01 0111 je nesmyslný sám pojem síťového
grafu. Buď se jedná o graf nebo o síť, což je zvláštní případ grafu. Protože
se však pojem síťový graf běžně používá a vznikl historicky, budeme jej
používat bez dalších komentářů. Výše uvedená norma definuje kritickou cestu
v síťovém grafu, jako cestu, která má nejdelší dobu trvání. Obě definice
jsou zcela ekvivalentní, ale námi uvedená definice obsahuje v sobě nepochybně
více informace.
V některých síťových grafech může být kritická cesta určena poměrně jednoduše,
jak uvidíte na jednoduchých příkladech, které budou v dalším textu uvedeny.
V reálných projektech, jako je např. výstavba atomové elektrárny, přehrady
apod. to již tak jednoduché není. Takovéto síťové grafy mohou mít i desetitisíce
hran.
Definice 3.22.
Časovou rezervou (rezervní dobou) nazýváme takový časový interval, o který
můžeme posunout ukončení práce nebo práci prodloužit, aniž by se změnila
celková doba dokončení projektu.
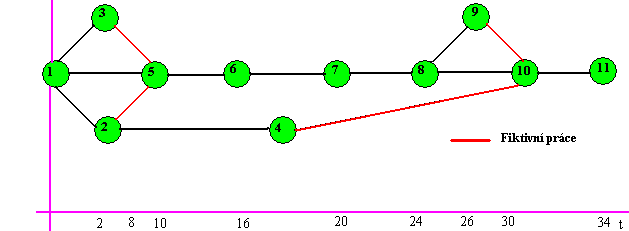
Na následujícím obrázku č.22 je zobrazen projekt v odpovídající časové
škále. Celková doba trvání projektu je rovna 34 jednotkám (obvykle se používá
jednotka týden, ale může to být i den apod.). Z obrázku je dále zřejmé,
že např. činnost (1,2) má celkovou rezervní dobu 8 jednotek, činnost (2,4)
22 jednotek atd.
Obr.22
Abychom mohli vypočítat rezervní doby jednotlivých činností, vypočteme
nejprve délku maximální cesty v síti (analogicky výpočtu nejkratší cesty
v Dantzigově verzi algoritmu Forda-Fulkersona) a potom stejně, jako jsme
určili trasu nejkratší cesty, určíme kritickou cestu v síťovém grafu. Při
přímém průchodu sítí získáme nejdříve možné začátky a nejdříve možné konce
jednotlivých prací, při zpětném průchodu nejpozději přípustné začátky a
konce. Pokud vztáhneme relativní čas ke konkrétní časové škále, získáme
kalendářní plán provádění jednotlivých činností, a o to nám vlastně jde.
Ohodnocení uzlu při přímém průchodu vzniká podle Dantzigova vztahu:
ESi = m a x {ESk + tki}
V tomto vztahu je i číslo uzlu, který ještě nebyl ohodnocen, k
je číslo uzlu, který již ohodnocen byl a tki je délka hrany,
spojující odpovídající uzly. V obrázku č.22 je třeba k tomu, abychom získali
hodnotu ES10 vzít maximální hodnotu z ES8 + 6 = 24 + 6
=30; ES9 + 0 = 26 + 0 = 26; ES4 + 0 = 8 + 0 = 8. Z toho
plyne, že skutečně ES10 = 30, tak jak je uvedeno na obrázku
22.
Analogický výpočet provádíme při zpětném průchodu sítí. V tomto případě
LFi = m i n {LFk - tjk }
V tomto vztahu je j číslo uzlu, který nebyl ještě při zpětném průchodu
ohodnocen, a LFj je nejpozději přípustná doba dokončení všech prací,
které končí v uzlu sítě j. Přitom ES1=0 a při zpětném
průchodu pro poslední uzel platí, že LFn = ESn.
Při takto ohodnocených vrcholech je možné vyjádřit i různé rezervní doby.
Celková rezervní doba se dá vyjádřit vztahem
TFij = LFj - ESi - tij
Definice 3.23.
Volná rezervní doba je počet časových jednotek, o které je možné posunout
nebo prodloužit činnost tak, aniž by se posunul nejdříve možný začátek
všech bezprostředně následujících prací.
RVij = ESj - ESi - tij
Poznámka.
Volná rezervní doba vzniká pouze v případě, kdy do některého uzlu ústí
ještě alespoň jedna hrana.
Definice 3.24.
Nezávislá rezervní doba je počet časových jednotek, o které lze nejvýše
prodloužit nebo posunout začátek činnosti, aniž se změní nejdříve možný
začátek všech bezprostředně následujících činností a nejpozději přípustný
konec činností, které bezprostředně předcházejí.
RNij = ESj - LFi - tij
Definice 3.25.
Závislá rezervní doba je počet časových jednotek, o které lze posunout
dobu zahájení činnosti nebo ji prodloužit, aniž se změní nejpozději přípustný
začátek všech bezprostředně následujících činností.
RZij = LFj - LFi - tij
Poznámka.
Závislou rezervu obyčejně nepočítáme. Při čerpání jednotlivých rezervních
dob postupujeme obvykle od nezávislé k volné a celkové rezervní době (
to proto, aby se již určený kalendářní plán nemusel příliš měnit). Pro
výpočet kritické cesty je podstatná pouze celková rezervní doba, ostatní
rezervy se využívají především při algoritmech přerozdělování a optimalizaci
zdrojů na síťových grafech.
Postup výpočtu realizujeme obvykle a) v matici
b) v grafu
c) v tabulce
Budeme se zabývat výpočtem v tabulce a výpočet na počítači provedeme rovněž
tímto způsobem. Máme pro to dva důvody. První je ten, že v reálných sítích
je výpočet v grafu nepřehledný a matice zabírá zbytečně moc místa v operační
paměti počítače.
Příklad.
Využijeme zadání, které je zobrazeno na obr. 22.
číslo
činnosti
|
činnost
od do
|
doba
trvání
|
ES
začátek
|
ES
konec
|
LS
začátek
|
LS
konec
|
TF
|
| 1
|
1-2
|
2
|
|
|
|
|
|
| 2
|
1-3
|
2
|
|
|
|
|
|
| 3
|
1-5
|
10
|
|
|
|
|
|
| 4
|
2-4
|
6
|
|
|
|
|
|
| 5
|
2-5
|
0
|
|
|
|
|
|
| 6
|
3-6
|
0
|
|
|
|
|
|
| 7
|
4-10
|
0
|
|
|
|
|
|
| 8
|
5-6
|
6
|
|
|
|
|
|
| 9
|
6-7
|
4
|
|
|
|
|
|
| 10
|
7-8
|
4
|
|
|
|
|
|
| 11
|
8-9
|
2
|
|
|
|
|
|
| 12
|
8-10
|
6
|
|
|
|
|
|
| 13
|
9-10
|
0
|
|
|
|
|
|
| 14
|
10-11
|
4
|
|
|
|
|
|
Předchozí tabulka zachycuje zadání dat. Pro pohodlný výpočet je dobré
1)mít uzly očíslované tak, aby číslo počátečního uzlu hrany bylo nižší
než číslo koncového uzlu (je zajištěna acykličnost grafu)
2) mít práce seřazeny lexikograficky podle počátečních a koncových uzlů
číslo
činnosti
|
činnost
od do
|
doba
trvání
|
ES
začátek
|
ES
konec
|
LS
začátek
|
LS
konec
|
TF
|
| 1
|
1-2
|
2
|
0
|
2
|
|
|
|
| 2
|
1-3
|
2
|
0
|
2
|
|
|
|
| 3
|
1-5
|
10
|
0
|
10
|
|
|
|
| 4
|
2-4
|
6
|
2
|
8
|
|
|
|
| 5
|
2-5
|
0
|
2
|
2
|
|
|
|
| 6
|
3-6
|
0
|
2
|
2
|
|
|
|
| 7
|
4-10
|
0
|
8
|
8
|
|
|
|
| 8
|
5-6
|
6
|
|
|
|
|
|
| 9
|
6-7
|
4
|
|
|
|
|
|
| 10
|
7-8
|
4
|
|
|
|
|
|
| 11
|
8-9
|
2
|
|
|
|
|
|
| 12
|
8-10
|
6
|
|
|
|
|
|
| 13
|
9-10
|
0
|
|
|
|
|
|
| 14
|
10-11
|
4
|
|
|
|
|
|
Tabulka se zaplňuje následujícím způsobem: práce, které začínají vrcholem
1 grafu, mohou být zahájeny ihned (to je v čase nula), tedy jejich nejdříve
možný začátek je v čase nula a nejdříve možný konec získáme tak,že k počátku
přičteme délku trvání činnosti. Viz předchozí tabulka.
Začátky dalších činností se získávají z konců prací v odpovídajícím uzlu
sítě. Např. činnost 1-2 končí v čase 2 a tedy práce 2-4 můče být nejdříve
zahájena v čase 2. Pokud v uvedeném uzlu končí více prací, pak bereme podle
vzorce maximální čas ukončení prací v daném uzlu (musí být dokončeny všechny
předcházející práce). V uzlu 5 končí práce 1-5 a 2-5. Jedna v čase
10, druhá v čase 2, práce 5-6 může být tedy zahájena až v čase 10.
číslo
činnosti
|
činnost
od do
|
doba
trvání
|
ES
začátek
|
ES
konec
|
LS
začátek
|
LS
konec
|
TF
|
| 1
|
1-2
|
2
|
0
|
2
|
|
|
|
| 2
|
1-3
|
2
|
0
|
2
|
|
|
|
| 3
|
1-5
|
10
|
0
|
10
|
|
|
|
| 4
|
2-4
|
6
|
2
|
8
|
|
|
|
| 5
|
2-5
|
0
|
2
|
2
|
|
|
|
| 6
|
3-6
|
0
|
2
|
2
|
|
|
|
| 7
|
4-10
|
0
|
8
|
8
|
|
|
|
| 8
|
5-6
|
6
|
10
|
16
|
|
|
|
| 9
|
6-7
|
4
|
16
|
20
|
|
|
|
| 10
|
7-8
|
4
|
20
|
24
|
|
|
|
| 11
|
8-9
|
2
|
24
|
26
|
|
|
|
| 12
|
8-10
|
6
|
24
|
30
|
|
|
|
| 13
|
9-10
|
0
|
26
|
26
|
|
|
|
| 14
|
10-11
|
4
|
30
|
34
|
|
|
|
V předchozí tabulce jsme dokončili přímý průchod síťovým grafem a vypočítali
kritickou dobu, kterou je maximální hodnota, kterou je ohodnocen poslední
vrchol grafu - vrchol s číslem 11. V našem případě má kritická dobo hodnotu
34 jednotek. Nyní přejdeme k zpětnému průchodu grafem a k výpočtu
nejpozději přípustných začátků a konců jednotlivých činností. Hodnota 34
je i nejpozději přípustným koncem všech prací, které končí ve vrcholu 11.
Od tohoto konce odvodíme začátky nejpozději přípustných prací tak, že odečteme
od konce délku práce. Tím dostaneme také nejpozději přípustný konec všech
prací, které končí ve vrcholu 10.
číslo
činnosti
|
činnost
od do
|
doba
trvání
|
ES
začátek
|
ES
konec
|
LS
začátek
|
LS
konec
|
TF
|
| 1
|
1-2
|
2
|
0
|
2
|
|
|
|
| 2
|
1-3
|
2
|
0
|
2
|
|
|
|
| 3
|
1-5
|
10
|
0
|
10
|
|
|
|
| 4
|
2-4
|
6
|
2
|
8
|
|
|
|
| 5
|
2-5
|
0
|
2
|
2
|
|
|
|
| 6
|
3-6
|
0
|
2
|
2
|
|
|
|
| 7
|
4-10
|
0
|
8
|
8
|
|
|
|
| 8
|
5-6
|
6
|
10
|
16
|
|
|
|
| 9
|
6-7
|
4
|
16
|
20
|
|
|
|
| 10
|
7-8
|
4
|
20
|
24
|
|
|
|
| 11
|
8-9
|
2
|
24
|
26
|
|
|
|
| 12
|
8-10
|
6
|
24
|
30
|
|
30
|
|
| 13
|
9-10
|
0
|
26
|
26
|
|
30
|
|
| 14
|
10-11
|
4
|
30
|
34
|
30
|
34
|
|
Pokud se dostaneme do situace, kdy je v jednom uzlu více různých nejpozději
přípustných začátků prací (např. u prací 11 a 12) , pak z hodnot těchto
začátků musíme vybrat minimální hodnotu - to proto, aby se do kritické
doby stačily vykonat všechny činnosti a tedy i jejich nejdelší posloupnost.
Z hodnot 24 a 28 vybereme tedy hodnotu 24 a tu doplníme jako nejpozději
přípustný konec prací, které končí ve vrcholu 8.
číslo
činnosti
|
činnost
od do
|
doba
trvání
|
ES
začátek
|
ES
konec
|
LS
začátek
|
LS
konec
|
TF
|
| 1
|
1-2
|
2
|
0
|
2
|
8
|
10
|
8
|
| 2
|
1-3
|
2
|
0
|
2
|
14
|
16
|
14
|
| 3
|
1-5
|
10
|
0
|
10
|
0
|
10
|
0
|
| 4
|
2-4
|
6
|
2
|
8
|
24
|
30
|
22
|
| 5
|
2-5
|
0
|
2
|
2
|
10
|
10
|
8
|
| 6
|
3-6
|
0
|
2
|
2
|
16
|
16
|
14
|
| 7
|
4-10
|
0
|
8
|
8
|
30
|
30
|
22
|
| 8
|
5-6
|
6
|
10
|
16
|
10
|
16
|
0
|
| 9
|
6-7
|
4
|
16
|
20
|
16
|
20
|
0
|
| 10
|
7-8
|
4
|
20
|
24
|
20
|
24
|
0
|
| 11
|
8-9
|
2
|
24
|
26
|
28
|
30
|
4
|
| 12
|
8-10
|
6
|
24
|
30
|
24
|
30
|
0
|
| 13
|
9-10
|
0
|
26
|
26
|
30
|
30
|
4
|
| 14
|
10-11
|
4
|
30
|
34
|
30
|
34
|
0
|
Celkové rezervní doby vypočteme podle vzorce. Kritické činnosti mají rezervní
dobu rovnu 0. Určitým druhem kontroly výpočtu je to, že se výpočet má zpětně
sešel v počátečním uzlu sítě. Musí vyjít alespoň jednou nejpozději přípustný
začátek ve vrcholu 1 roven 0.
Určitým problémem, který jsme obešli, je číslování vrcholů. Pravidlo, které
jsme uvedli, říká, že hrany musí být číslovány tak, aby číslo počátečního
vrcholu hrany bylo menší než číslo koncového vrcholu hrany. Takové číslování
zaručuje, že graf je acyklický ( neobsahuje žádný cyklus a je tedy správný
z logického hlediska - jinak by zahájení činnosti muselo čekat na svůj
vlastní konec, což je nesmysl). Ve velkých reálných sítích však velmi často
vznikají situace, kdy je třeba doplnit do sítě další práce a není dosti
dobře myslitelné, aby při každém tomto doplnění bylo provedeno přečíslování
grafu. Je proto třeba vytvořit nějaký algoritmus, který by případně mohl
být realizován na počítači, a který by tento problém vyřešil. Postup při
přečíslování může být následující:
1. V síti najdeme vrchol, do kterého nevede žádná hrana a označímeho číslem
1. Takový vrchol musí existovat, jinak by graf obsahoval cyklus.
2. Označíme všechny vrcholy grafu, do kterých je možné se dostat po orientovaných
hranách z již očíslovaných vrcholů, z nich vybereme ty, do kterých nevedou
hrany z vrcholů ještě neočíslovaných a některému přidělíme následující
číslo po posledním již přiděleném.
Krok 2 opakujeme do té doby, dokud existují neočíslované vrcholy. Algoritmus
může být předčasně ukončen, nelze-li označit vrchol. V takovém případě
je graf nesouvislý nebo neexistuje cesta z počátku do konce.To znamená,
že graf je špatně sestaven nebo nelze vybrat z označených vrcholů žádný,
do kterého by neústila hrana z ještě neočíslovaných vrcholů, graf obsahuje
cyklus a je logicky špatně sestaven.
Příklad.
Obr.23
Předchozí obrázek ukazuje postup přečíslování vrcholů sítě.
Znakem + jsou zobrazeny označené vrcholy, které mohou být perspektivně
očíslovány. V dalším obrázku je již číslování dokončeno.
 Obr.24
Obr.24
Na následujícím obrázku je znázorněna situace. Síť je zadána nesprávně
a nelze očíslovat již žádný další vrchol sítě, síť obsahuje cyklus
Obr.25
Existuje i jiný způsob přečíslování uzlů sítě a to takový, že pokud narazíme
na hranu, která naší podmínce nevyhovuje, vyměníme očíslování vrcholů
Příklad.
Nechť je zadána síť výčtem hran, které nevyhovují naší podmínce. Např.:
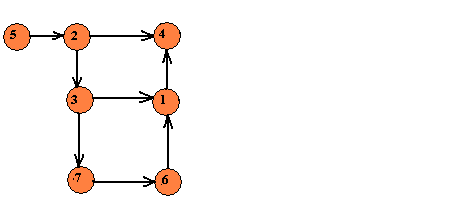
Obr.26
| 5
|
2
|
|
2
|
5
|
|
2
|
3
|
| 2
|
3
|
|
5
|
3
|
|
3
|
5
|
| 3
|
1
|
|
3
|
1
|
|
5
|
1
|
| 6
|
1
|
|
6
|
1
|
|
6
|
1
|
| 2
|
4
|
|
5
|
4
|
|
3
|
4
|
| 3
|
7
|
|
3
|
7
|
|
5
|
7
|
| 7
|
6
|
|
7
|
6
|
|
7
|
6
|
| 1
|
4
|
|
1
|
4
|
|
1
|
4
|
Jako první se narušuje pravidlo u první dvojice vrcholů, zaměníme tedy
všude dvojku a pětku. Nyní došlo k záměně u druhé hrany 5,3 zaměníme tedy
čísla 5 a 3 a vznikne tabulka následující Stejným způsobem můžeme pokračovat
i dále. Tato metoda je pro ruční práci neefektivní, ale poměrně snadno
se programuje.
3.9.3. Optimalizace síťových grafů.
Po výpočtu parametrů síťového grafu a určení kalendářního plánu jednotlivých
činností je třeba provést tzv. optimalizaci síťového grafu. Pod pojmem
optimalizace v tomto případě rozumíme každé zlepšení v komplexu
činností s ohledem na doby jejich trvání a na racionální využití různých
zdrojů. Z praktického hlediska rozlišujeme časovou optimalizaci, cenovou
a proudovou.Časovou optimalizací provádíme zkrácení délky kritické cesty
především zkrácením délky kritických prací, změnou topologie sitě a jemnějším
členěním prací. Zkrácení kritických prací dosahujeme zkvalitněním jejich
realizace, změnou technologie, zlepšením zásobování, racionalizací pracovních
míst a také redislokací zdrojů z nekritických prací na práce kritické.
Analýza zdrojů je jedním z velmi důležitých ekonomických faktorů při plánování
projektu. Zdroje je možné rozdělit zhruba do tří základních skupin:
- PRACOVNÍ SÍLY
- FINANČNÍ ZDROJE
- MATERIÁLOVÉ ZDROJE
Definice 3.26.
Intenzita spotřeby zdroje je spotřeba zdroje za časovou jednotku.
Aby bylo co optimalizovat, je třeba nejdříve určit úroveň nezbytných zdrojů.
To provádíme následujícím způsobem:
A) Vypočítáme kritickou cestu a určíme nejdříve možné a nejpozději přípustné
začátky a konce jednotlivých činností.
B) Sestavíme síťový graf v časové stupnici.
C) Vyjasníme celkovou intenzitu spotřeby zdroje pro každý časový interval.
Sestavíme Ganttův diagram spotřeby zdrojů podle nejdříve možných a nejpozději
přípustných začátků a konců jednotlivých činností. V případě potřeby přerozdělíme
zdroje.( O tom, jak vypadá Ganttův diagram bude řeč později.)
Definice 3.27.
Optimálním rozdělením zdrojů rozumíme takové časové rozmístění jednotlivých
činností, které zabezpečí při zadané intenzitě spotřeby zdrojů ukončení
projektu v minimálním čase.
Pokud je autorovi známo, nebyly publikovány efektivní metody řešení tohoto
problému, které by dávaly optimální řešení a současně umožňovaly řešit
dostatečně složité síťové grafy. Hodně se v praxi používají heuristické
- suboptimální algoritmy a metody. Jedním z nich je i následující algoritmus:
KROK 1. Pro každou práci určíme nejdříve možný a nejpozději přípustný začátek
a konec a celkovou rezervní dobu, případně nezávislou a vázanou rezervu.
KROK 2. Vytvoříme síťový graf v časovém měřítku. Určíme intenzity spotřeby
pro každý časový interval. Jestliže pro časový interval je splněno omezení
na spotřebu zdroje, pak v daném časovém intervalu považujeme optimalizaci
za ukončenou. Jestliže tomu tak není, pak přecházíme k následujícímu kroku
algoritmu.
KROK 3. Pro provedení korekce očíslujeme práce v tomto intervalu podle
růstu jejich celkových rezervních dob. Při stejných rezervních dobách pak
podle poklesu jejich intenzit. Započaté práce považujeme za nejdůležitější.
Činnosti realizujeme v této škále pouze potud, pokud jsou k dispozici pro
jejich provedení dostatečné zdroje.
KROK 4. Celý postup opakujeme pro následující časový interval.
Pro urychlení korekce prací je obyčejně nejdříve určena monotonně rostoucí
posloupnost nejdříve možných začátků a konců s projekcí na vodorovnou časovou
osu.
Příklad.
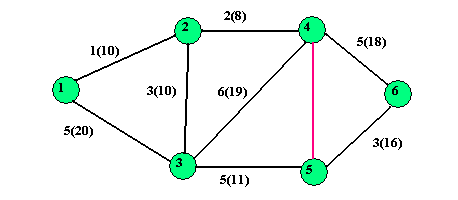
Obr.27
U síťového grafu na obr.27 jsou v závorkách uvedeny intenzity spotřeby
pracovní síly. Určíme nejprve kalendářní plán a rezervní doby jednotlivých
činností.
| činnost
|
doba
trvání
|
spotř.
zdroje
|
ES
začátek
|
ES
konec
|
LF
začátek
|
LF
konec
|
TF
|
| 1-2
|
1
|
10
|
0
|
1
|
1
|
2
|
1
|
| 1-3
|
5
|
20
|
0
|
5
|
0
|
5
|
0
|
| 2-3
|
3
|
10
|
1
|
4
|
2
|
5
|
1
|
| 2-4
|
2
|
8
|
1
|
3
|
9
|
11
|
8
|
| 3-4
|
6
|
19
|
5
|
11
|
5
|
11
|
0
|
| 3-5
|
5
|
11
|
5
|
10
|
8
|
13
|
3
|
| 4-5
|
0
|
0
|
11
|
11
|
13
|
13
|
2
|
| 4-6
|
5
|
18
|
11
|
16
|
11
|
16
|
0
|
| 5-6
|
3
|
16
|
11
|
14
|
13
|
16
|
2
|
Obr.28
Nyní můžeme přejít k sestrojení Ganttova diagramu.
Obr.29
Předpokládejme, že je třeba vyrovnat spotřebu pracovních sil tak, aby po
celou dobu realizace projektu nepřekročila 30 jednotek. Je vidět, že v
prvém časovém úseku je vše v naprostém pořádku a práce tam mohou probíhat
podle nejdříve možných začátků a konců. V druhém časovém intervalu 1-3
je již situace jiná a je zde třeba provést vyrovnání zdroje. Ukončena je
práce 1-2, probíhá práce 1-3 a mají být zahájeny práce 2-3 s rezervou 1
a počtem pracovníků 10 a práce 2-4 s rezervou 8 a počtem pracovníků 8.
Do limitu 30 zdroje se nám vejde jen práce 2-3 a práce 2-4 bude muset počkat
na svoje zahájení až do časového okamžiku 4, kdy bude dokončena práce 2-3
a uvolněny odpovídající zdroje. V tabulce se tato situace projeví následovně:
| činnost
|
doba
trvání
|
spotř.
zdroje
|
ES
začátek
|
ES
konec
|
LF
začátek
|
LF
konec
|
TF
|
| 1-2
|
1
|
10
|
0
|
1
|
1
|
2
|
1
|
| 1-3
|
5
|
20
|
0
|
5
|
0
|
5
|
0
|
| 2-3
|
3
|
10
|
1
|
4
|
2
|
5
|
1
|
| 2-4
|
2
|
8
|
4!!!
|
6!!!
|
9
|
11
|
5!!!
|
| 3-4
|
6
|
19
|
5
|
11
|
5
|
11
|
0
|
| 3-5
|
5
|
11
|
5
|
10
|
8
|
13
|
3
|
| 4-5
|
0
|
0
|
11
|
11
|
13
|
13
|
2
|
| 4-6
|
5
|
18
|
11
|
16
|
11
|
16
|
0
|
| 5-6
|
3
|
16
|
11
|
14
|
13
|
16
|
2
|
Dalším časovým intervalem je interval 4-5,ve kterém je vše v pořádku,
spotřeba zde tvoří 28 jednotek, v časovém intervalu 5-6 je to 38 jednotek.
To již v pořádku není a je nutno v optimalizaci pokračovat. Práce 2-4
musí probíhat a posunout je možné pouze práce 3-4 a 3-5. První práce je
kritická s rezervou 0 a druhá má rezervu 3. Musíme tedy začátek práce 3-5
posunout k časovému okamžiku 6, kdy skončí práce 2-4 a uvolní odpovídající
zdroje. Spotřeba zdroje tedy bude v intervalu 5-6 27 jednotek a v intervalu
6-11 30 jednotek. Další problémy začnou až v intervalu 11-14, kde spotřeba
činí 34 jednotek. Práce 4-6 je kritická s rezervou 0 a práce 5-6 má rezervu
pouze 2 jednotky,ovšem její zahájení je možné posunout až k času 16 t.j
o 5 jednotek,což je víc než dovoluje rezervní doba. To znamená, že je třeba
přepočítat síťový graf, protože by mohla vzniknout jiná kritická cesta
a jiné rezervní doby.
| činnost
|
doba
trvání
|
spotř.
zdroje
|
ES
začátek
|
ES
konec
|
LF
začátek
|
LF
konec
|
TF
|
| 1-2
|
1
|
10
|
0
|
1
|
1
|
2
|
1
|
| 1-3
|
5
|
20
|
0
|
5
|
0
|
5
|
0
|
| 2-3
|
3
|
10
|
1
|
4
|
2
|
5
|
1
|
| 2-4
|
2
|
8
|
4!!!
|
6!!!
|
9
|
11
|
5!!!
|
| 3-4
|
6
|
19
|
5
|
11
|
5
|
11
|
0
|
| 3-5
|
5
|
11
|
6!!!
|
11!!!
|
8
|
13
|
2!!!
|
| 4-5
|
0
|
0
|
11
|
11
|
13
|
13
|
2
|
| 4-6
|
5
|
18
|
11
|
16
|
14
|
19
|
3!!!
|
| 5-6
|
3
|
16
|
16
|
19
|
16
|
19
|
0!!!
|
Práce 4-5 a předcházející není třeba zpětně přepočítávat, protože již probíhají
nebo dokonce proběhly, také jejich rezervy jsou již bezpředmětné, protože
v jejich rámci již není možno s činnostmi pohybovat (mohlo by dojít k opětné
kumulaci zdroje). Smysl mají pouze sloupce s nejdříve možnými začátky a
konci jednotlivých prací!!!
Zobrazme nyní nový průběh spotřeby zdroje v Ganttově diagramu:
Obr.30
Následně se můžeme pokusit předisponovat pracovníky z jiných prací na některé
kritické práce a snížit tak jejich dobu trvání, ne vždy je to však možné.Práce
5-6 má dvě rezervní jednotky a můžeme se tedy pokusit odebrat z ní čtyři
pracovníky. Jejich předisponováním na práci 4-6 dosáhneme následující situace:

Obr 30
Pro vyrovnávání spotřeby více než jednoho zdroje lze použít analogický
algoritmus. Práce bude posunuta, jestliže alespoň jeden ze zdrojů překročí
limit.